Bộ đề thi thử vào lớp 10 năm 2019 - 2020 phòng GD&ĐT Quận 11, Hồ Chí Minh 4 Đề thi vào lớp 10 năm 2019 môn Toán
Mời các bạn cùng tham khảo Bộ đề thi thử vào lớp 10 năm 2019 - 2020 phòng GD&ĐT Quận 11, Hồ Chí Minh để chuẩn bị cho kỳ thi tuyển sinh vào lớp 10 sắp tới của mình.
Hi vọng, tài liệu này sẽ giúp ích nhiều trong việc luyện tập và củng cố kiến thức môn Toán đề chuẩn bị tốt cho kì thi vào lớp 10 sắp tới. Sau đây là nội dung chi tiết, mời các bạn cùng tham khảo.
Đề thi vào lớp 10 năm 2019 môn Toán
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO QUẬN 11
ĐỀ THAM KHẢO TUYỂN SINH LỚP 10 NĂM HỌC 2019-2020
Bài 1:
a) Vẽ đồ thị Parabol (P) của hàm số
4
x
y
2
và đường thẳng (D): y = x + 1 trên cùng
một hệ trục tọa độ.
b) Chứng tỏ bằng phép toán (P) và (D) tiếp xúc nhau tại một điểm. Tìm tọa độ tiếp điểm
này.
Bài 2: Cho phương trình x
2
+ x – 2 – m
2
= 0 (x là ẩn, m là tham số)
a/ Chứng minh phương trình luôn có 2 nghiệm phân biệt x
1
,x
2
với mọi m.
b/ Với giá trị nào của m thì nghiệm PT thỏa hệ thức
2
3
2
1
x
x
Bài 3: Một chiếc máy bay bay lên với vận tốc 520 km/h. Đường bay lên tạo với
phương nằm ngang một góc 24
0
. Hỏi sau 90 giây máy bay lên cao được bao nhiêu
km theo phương thẳng đứng? ( kết quả làm tròn đến chữ số thập phân thứ nhất)
Bài 4:
Hai chiếc tàu thủy B và C cùng xuất phát từ một vị trí
A, đi thẳng theo 2 hướng tạo thành 1 góc 60
0
. Tàu B
chạy với vận tốc 40 hải lý một giờ, tàu C chạy với vận
tốc 30 hải lý một giờ. Hỏi sau 1,5 giờ hai tàu B và C
cách nhau bao nhiêu hải lý? Biết rằng 1 hải lý xấp xỉ
1,852km. ( kết quả trung gian làm tròn đến chữ số thập
phân thứ hai)
Bài 5:
Một người mang 1 xấp tiền 20 tờ gồm 2 loại 100 000 đồng và 200 000 đồng đi
siêu thị. Sau khi thanh toán hoá đơn 2 650 000 đồng, người đó kiểm tra thấy số tiền còn
thừa lại trong túi là 150 000 đồng. Hỏi khi đi người đó mang theo bao nhiêu tờ mỗi loại?
A
B
D
C
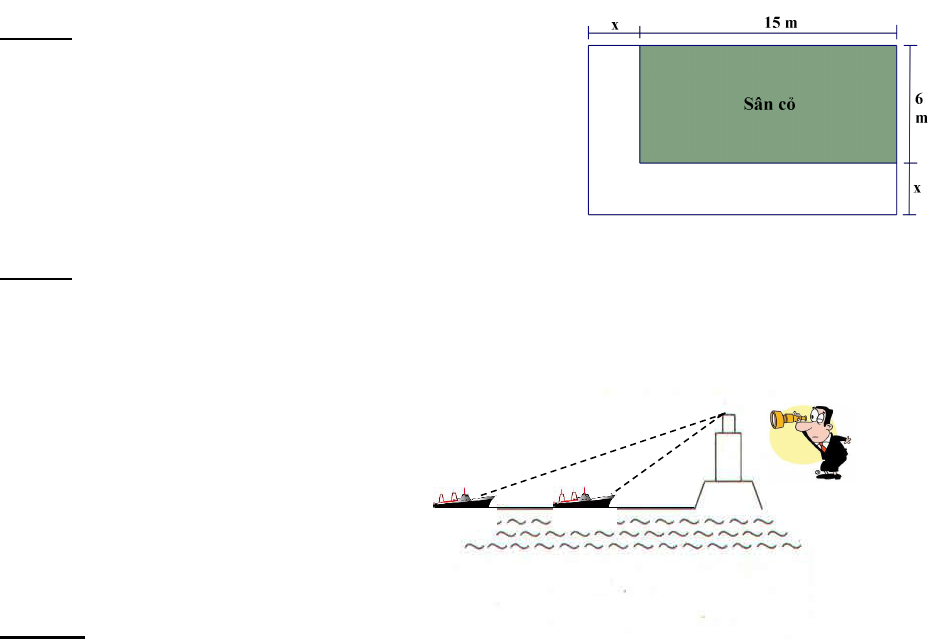
Bài 6: Người ta làm một lối đi theo chiều dài và
chiều rộng của một sân cỏ hình chữ nhật như hình.
Em hãy tính chiều rộng x của lối đi. Biết rằng lối đi
có diện tích bằng 46 m
2
, sân cỏ có chiều dài 15 m,
chiều rộng 6 m.
Bài 7: Từ đài quan sát cao 10m, Nam có thể nhìn thấy 2 chiếc thuyền dưới góc 45
0
và 30
0
so với phương ngang. Hãy tính khoảng cách 2 chiếc thuyền, làm tròn đến chữ số thập
phân thứ nhất. (điều kiện lý tưởng : vị trí 2 chiếc thuyền và vị trí đài quan sát thẳng hàng)
Bài 8 : Cho tam giác ABC nhọn ( AB < AC) có đường cao AH. Vẽ đường tròn tâm
(O) đường kính AB cắt AC tại I. Gọi E là điểm đối xứng của H qua AC, EI cắt AB
tại K và cắt (O) tại điểm thứ hai là D.
a) Chứng minh tứ giác ADHB nội tiếp và AD = AE.
b) Chứng minh DH
AB. Suy ra HA là phân giác của góc IHK.
c) Chứng minh 5 điểm A, E, C, H, K cùng thuộc đường tròn .
===============HẾT================
Đáp án :
Bài 1 :
Vẽ (P) và bảng giá trị đúng.
Vẽ (D) và bảng giá trị đúng.
Phương trình hoành độ giao điểm của (P) và (D) là
1x
4
x
2
x
2
+ 4x + 4 = 0
0
x = –2 y = –1.
Tọa độ tiếp điểm của (P) và (D) là (–2 ; –1).
Bài 2:
a/ a = 1 > 0
c = – (2+m
2
) <0
vậy ac <0 : Pt luôn có 2 nghiệm phân biệt với mọi m .
b/ Theo vi-ét ta có x
1
+x
2
= –1
x
1
x
2
= – 2 – m
2
Ta có: 2x
1
+3x
2
= 0
–2+ x
2
= 0
x
2
= 2
x
2
là nghiệm của pt x
2
+ x – 2 – m
2
= 0
4– m
2
=0
m = 2; –2
Bài 3:
Đổi 90s =
1
h
40
Tính được AB = 13km
Tính đúng BC = AB. sinA = 13.sin24
0
5,3 km
Kết luận:
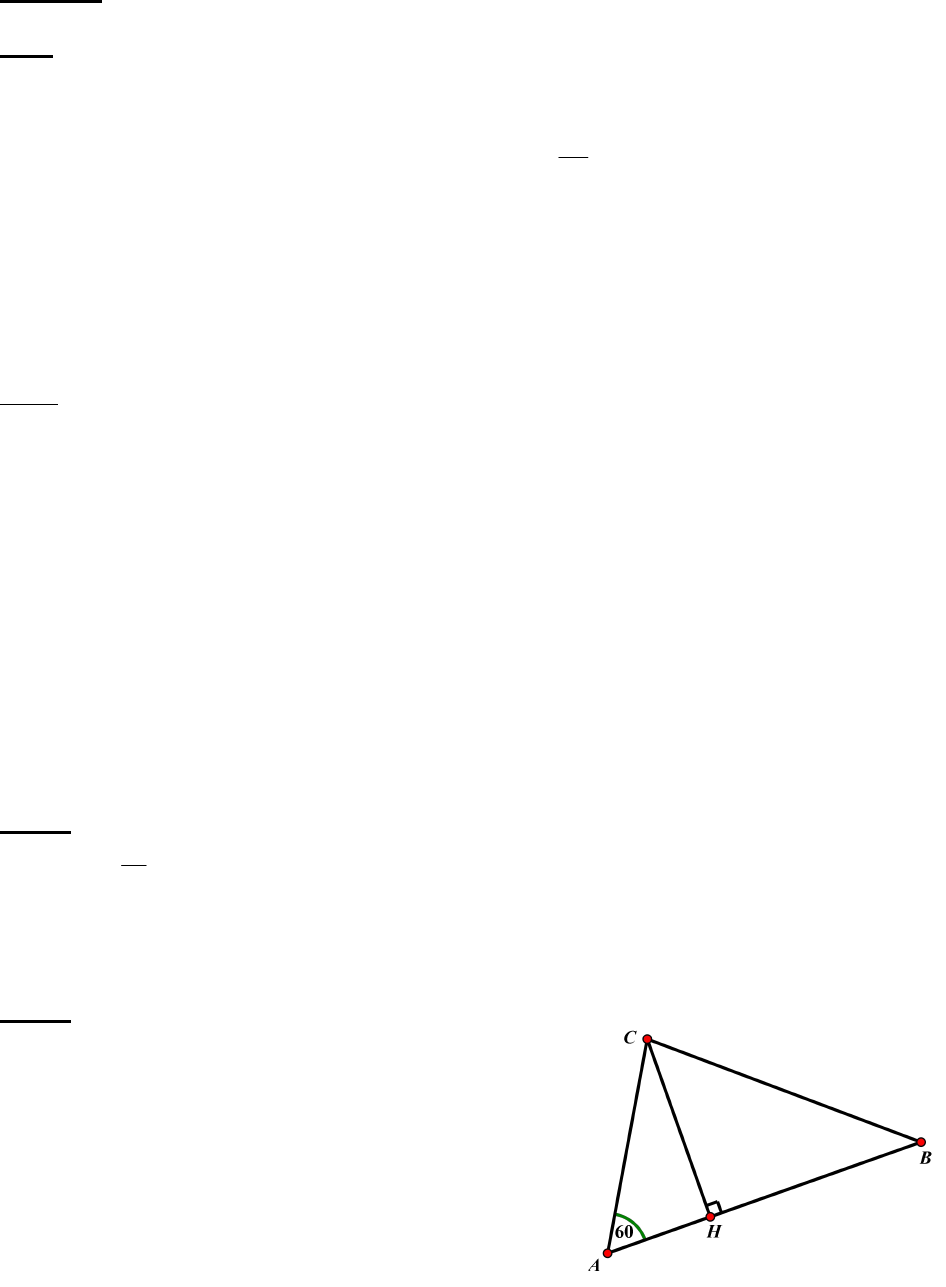
Bài 4:
v
B
= 40M/h = 74,08km/h
v
C
= 30M/h = 55,56km/h
S
AC
= 1,5. 74,08 = 111,12 km.
S
AB
= 1,5 . 55,56 = 83,34 km.
Vẽ CH
AB tại H.
ACH vuông tại H có
CH = AC. sinA = 111,12 . sin60
0
= 96,23.
AH = AC. cosA = 111,12 . cos 60
0
= 55,56
HB = AB – AH = 83,34 – 55,56 = 27,28
Tính đúng BC = 100,02km = 54 hải lý.
KL : Vậy sau 1,5 giờ 2 tàu cách nhau 54 hải lý.
Chia sẻ bởi: 
Trịnh Thị Thanh
Trịnh Thị Thanh Liên kết tải về
Link Download chính thức:
Bộ đề thi thử vào lớp 10 năm 2019 - 2020 phòng GD&ĐT Quận 11, Hồ Chí Minh Download
Có thể bạn quan tâm
-
Thuyết minh về cây bút chì (Dàn ý + 9 mẫu)
-
Văn mẫu lớp 8: Phân tích bài thơ Ngắm trăng của Hồ Chí Minh (Sơ đồ tư duy)
-
Bài dự thi những tấm gương tâm huyết sáng tạo học theo lời Bác năm 2023
-
Tập làm văn lớp 5: Tả cảnh bình minh trên quê hương em
-
Văn mẫu lớp 7: Cảm nghĩ về ngày Tết cổ truyền quê em
-
Văn mẫu lớp 9: Đóng vai ngư dân kể lại bài thơ Đoàn thuyền đánh cá
-
Bài thơ Lượm - Sáng tác năm 1949, Tố Hữu
-
Mẫu 09/ĐK: Đơn đăng ký biến động đất đai
-
Tranh tô màu Pikachu - Bộ tranh tô màu Pikachu đẹp
-
Giáo án Toán lớp 1 (Sách mới) - Giáo án Toán lớp 1 (trọn bộ 5 sách)
Sắp xếp theo
