Bộ đề thi thử THPT Quốc gia 2020 trường THPT Chuyên Thái Bình Đề minh họa THPT Quốc gia năm 2020 môn Toán
Ngày thi THPT Quốc gia 2020 đang ngày một đến gần, Eballsviet.com xin giới thiệu đến các bạn tài liệu Đề thi thử THPT Quốc gia 2020 trường THPT Chuyên Thái Bình.
Hy vọng đây là tài liệu bổ ích giúp các bạn học sinh lớp 12 rèn luyện kỹ năng làm bài và làm quen với cấu trúc đề thi. Nội dung chi tiết mời các bạn cùng tham khảo và tải tài liệu tại đây.
Đề thi thử THPT Quốc gia 2020 môn Toán
Trang 1/6 - Mã đề thi 210
SỞ GIÁO DỤC & ĐÀO TẠO THÁI BÌNH
TRƯỜNG THPT CHUYÊN THÁI BÌNH
ĐỀ THI THỬ THPTQG LẦN I – NĂM HỌC: 2019 - 2020
MÔN TOÁN
Thời gian làm bài: 90 phút
(50 câu trắc nghiệm)
Họ và tên thí sinh: ........................................................ Lớp: ............. SBD: ....................
Câu 1: Rút gọn biểu thức
7
3
5
3
7
4 2
.
.
a a
A
a a
với
0
a
. Khẳng định nào sau đây đúng?
A.
2
7
A a
. B.
2
7
A a
. C.
7
2
A a
. D.
7
2
A a
.
Câu 2: Cho hàm số
2sin cosy x x
. Đạo hàm của hàm số là:
A.
2cos sinx x
. B.
2cos siny x x
.
C.
2cos siny x x
. D.
2cos siny x x
.
Câu 3: Hàm số nào trong bốn hàm số liệt kê ở dưới nghịch biến trên từng khoảng xác định của nó?
A.
2 1
e
2
x
y
. B.
1
3
x
y
C.
3
e
x
y
. D.
2017
x
y .
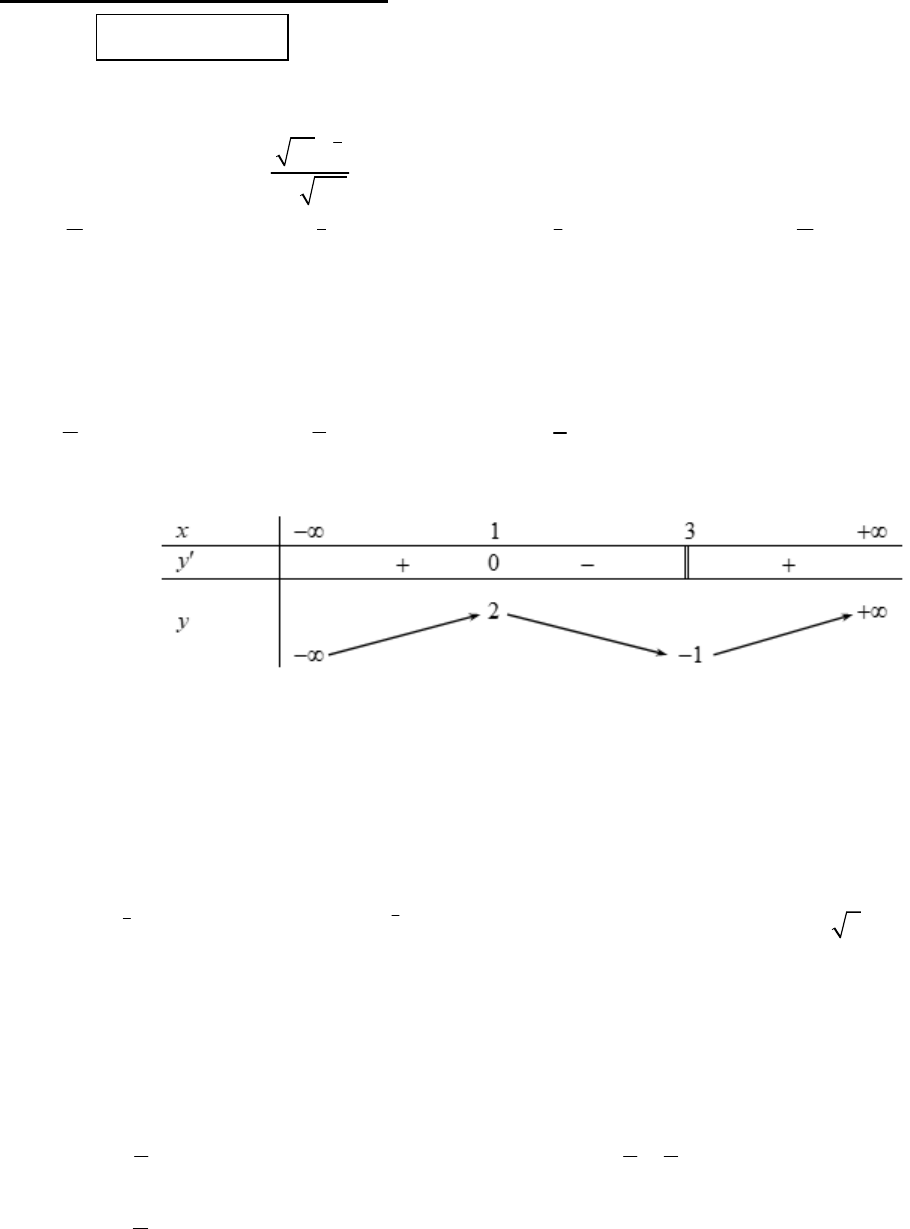
Câu 4: Cho hàm số
y f x
liên tục trên
và có bảng biến thiên như sau:
Khẳng định nào sau đây đúng?
A. Hàm số đạt cực tiểu tại điểm
3
x
. B. Hàm số có giá trị nhỏ nhất trên
bằng
1
.
C. Hàm số có giá trị cực đại bằng
1
. D. Hàm số chỉ có một điểm cực trị.
Câu 5: Hình bát diện đều có bao nhiêu cạnh?
A.
16
. B.
8
. C.
24
. D.
12
.
Câu 6: Trong các hàm số sau đây, hàm số nào xác định với mọi giá trị thực của
x
?
A.
1
3
2 1
y x
. B.
1
2
3
2 1
y x
. C.
3
1 2
y x
. D.
3
1 2
y x
.
Câu 7: Công thức tính diện tích xung quanh của hình nón tròn xoay có bán kính đáy
r
và độ dài đường
sinh
l
là:
A.
xq
S
rl
. B.
2
xq
S
rl
. C.
xq
S
rl
. D.
2
xq
S
rl
Câu 8: Cho các số thực dương
,a b
với
1a
. Tìm mệnh đề đúng trong các mệnh đề dưới đây.
A.
2
1
log log
2
a
a
ab b
. B.
2
1 1
log log
2 2
a
a
ab b
.
C.
2
1
log log
4
a
a
ab b
. D.
2
log 2 2 log
a
a
ab b
.
Câu 9: Cho hàm số
( )y f x
có đạo hàm trên
và
'( ) 0 (0; )
f x x
. Biết
(1) 2020
f
. Khẳng
định nào dưới đây đúng?
A.
2020 2022
f f
. B.
(2018) (2020)
f f
.
C.
(0) 2020
f
. D.
(2) (3) 4040
f f
.
Câu 10: Cho hình chóp
.
S ABC
có
, ,SA SB SC
đôi một vuông góc. Biết
SA SB SC a
, tính thể tích
của khối chóp
.
S ABC
.
MÃ ĐỀ 210
Trang 2/6 - Mã đề thi 210
A.
3
6
a
. B.
3
3
4
a
. C.
3
2
a
. D.
3
3
a
.
Câu 11: Tổng
0 1 2 2 3 3
3 3 3 ... ( 1) .3
n n n
n n n n n
S C C C C C
bằng:
A.
2
n
B.
( 2)
n
C.
4
n
D.
2
n
Câu 12: Cho 10 điểm phân biệt. Hỏi có thể lập được bao nhiêu vectơ khác
0
mà điểm đầu và điểm cuối
thuộc 10 điểm đã cho.
A.
2
10
C
. B.
2
10
A
. C.
2
8
A
. D.
1
10
A
.
Câu 13:
Cho hàm số
y f x
có bảng biến thiên như hình bên dưới. Hỏi đồ thị hàm số đã cho có tất cả
bao nhiêu đường tiệm cận đứng và ngang?
A.
3
. B.
1
. C.
2
. D.
4
.
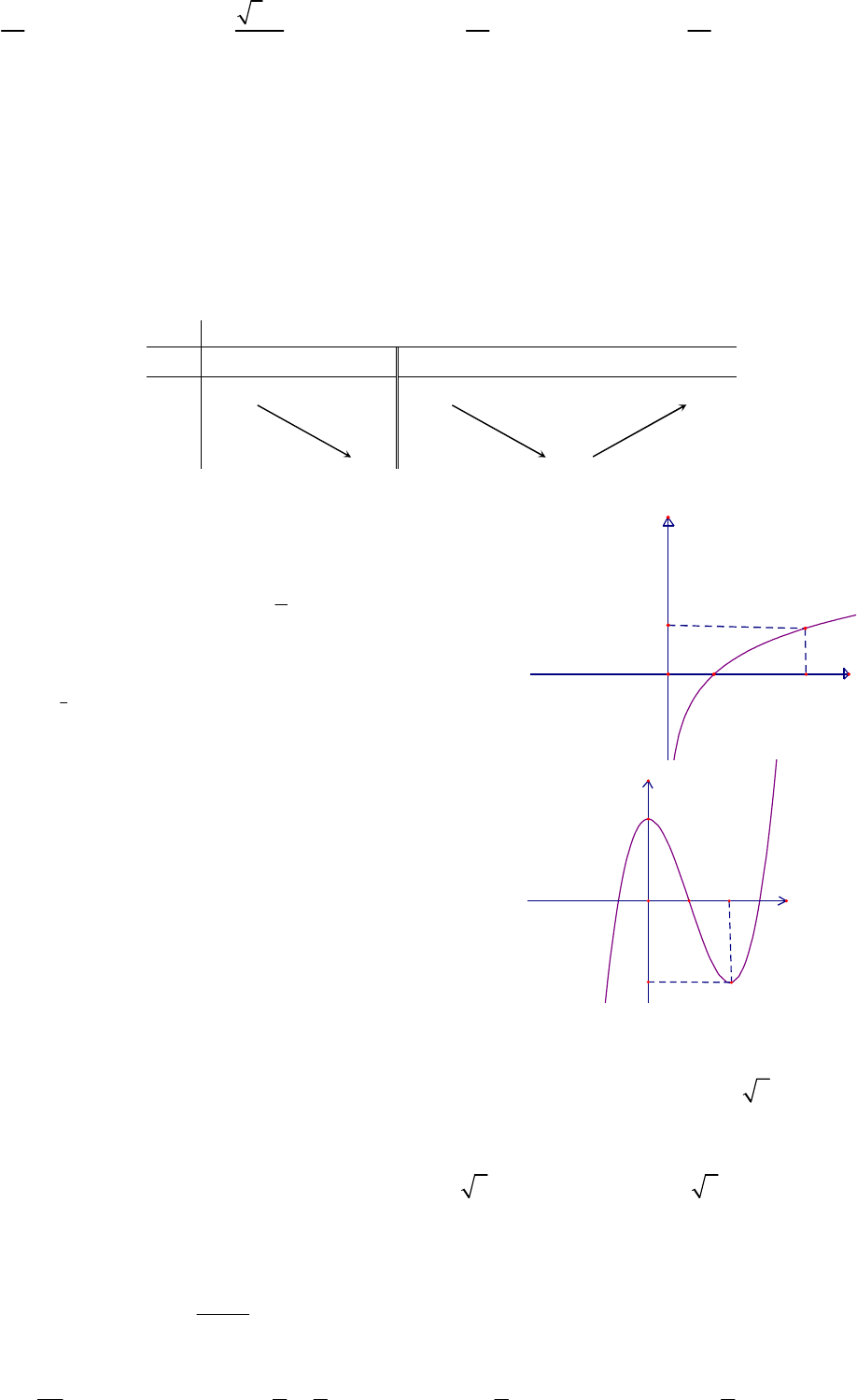
Câu 14: Hàm số nào dưới đây có đồ thị như trong hình vẽ
bên?
A.
2
x
y
. B.
1
3
x
y
.
C.
1
3
logy x
. D.
3
logy x
.
0
1
x
y
3
1
Câu 15: Đường cong trong hình vẽ bên là đồ thị của hàm
số nào trong các hàm số dưới đây?
A.
3 2
3 2
y x x
.
B.
3 2
3 2
y x x
.
C.
3
3 2y x x
.
D.
4 2
2 2
y x x
.
2
0
1
x
y
2
-2
Câu 16: Hàm số
4 2
3
y x x
có mấy điểm cực trị?
A.
1
. B.
2
. C.
3
. D.
0
.
Câu 17: Cho hình lập phương
.
ABCD A B C D
có diện tích mặt chéo
ACC A
bằng
2
2 2a
. Thể tích
của khối lập phương
.
ABCD A B C D
là:
A.
3
a
B.
3
2a
C.
3
2a
D.
3
2 2a
Câu 18: Tìm số giao điểm của đồ thị hàm số
3
3 3y x x
và đường thẳng
y x
.
A.
1
. B.
2
. C.
3
. D.
0
.
Câu 19. Cho hàm số
2 1
1
x
y
x
có đồ thị
C
và đường thẳng
: 2 3d y x
. Đường thằng
d
cắt
( )C
tại
hai điểm
A
và
B
. Tọa độ trung điểm của đoạn
AB
là:
A.
3
; 6
2
M
. B.
3 3
;
4 2
M
. C.
3
;0
2
M
. D.
3
;0
4
M
.
x
1
2
y
0
y
3
2
5
Trang 3/6 - Mã đề thi 210
Câu 20: Hàm số
2
2
log 2y x x
nghịch biến trên khoảng nào sau đây?
A.
;1
. B.
;0
. C.
1;1
. D.
0;
.
Câu 21: Hai đường tiệm cận của đồ thị hàm số
2 1
1
x
y
x
tạo với hai trục tọa độ một hình chữ nhật có
diện tích bằng bao nhiêu?
A.
2
. B.
1
. C.
3
. D.
4
.
Câu 22: Cho mặt cầu
( ; )S I R
và mặt phẳng
( )P
cách
I
một khoảng bằng
2
R
. Khi đó thiết diện của
( )P
và
S
là một đường tròn có bán kính bằng:
A.
R
. B.
3
2
R
. C.
3R
D.
2
R
Câu 23: Gọi
m
,
M
lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số
1
1
2
f x x x
trên
đoạn
0;3
. Tính tổng
2
S M m
.
A.
0
S
. B.
3
2
S
. C.
2
S
. D.
4
S
.
Câu 24: Hàm số:
3 2
3 9 7
y x x x
đồng biến trên khoảng nào sau đây?
A.
1;y
. B.
5; 2
. C.
;1
. D.
1;3
.
Câu 25: Viết phương trình tiếp tuyến của đồ thị
3
( ) : 2 lnC y x x x
tại điểm
(1;2)
M
.
A.
7 9y x
. B.
3 4
y x
. C.
7 5y x
. D.
3 1y x
.
Câu 26: Cho hình chóp
.
S ABC
có đáy
ABC
là tam giác đều cạnh
a
, cạnh bên
SA
vuông góc với đáy,
SA a
. Thể tích của khối chóp
.
S ABC
bằng:
A.
3
3
4
a
. B.
3
3
6
a
. C.
3
4
a
. D.
3
3
12
a
.
Câu 27: Hai anh em A sau Tết có
20 000 000
đồng tiền mừng tuổi. Mẹ gửi ngân hàng cho hai anh em
với lãi suất
0,5
/tháng (sau mỗi tháng tiền lãi được nhập vào tiền gốc để tính lãi tháng sau). Hỏi sau
1
năm hai anh em được nhận bao nhiêu tiền biết trong một năm đó hai anh em không rút tiền lần nào (số
tiền được làm tròn đến hàng nghìn)?
A.
21 233 000
đồng. B.
21 234 000
đồng.
C.
21 235 000
đồng. D.
21 200 000
đồng.
Câu 28: Cho khối chóp .
S ABCD
có thể tích bằng
3
4a
, đáy ABCD là hình bình hành. Gọi là
M
trung
điểm của cạnh
SD
. Biết diện tích tam giác SAB bằng
2
.a
Tính khoảng cách từ
M
tới mặt phẳng
( )SAB
.
A.
12a
.
B.
6 .a
C.
3 .a
D.
4 .a
Câu 29: Cho
a
và
b
là các số thực dương khác
1
. Biết
rằng bất kì đường thẳng nào song song với trục tung mà
cắt các đồ thị
log
a
y x
,
log
b
y x
và trục hoành lần
lượt tại
A
,
B
và
H
phân biệt ta đều có
3 4
HA HB
(hình vẽ bên dưới). Khẳng định nào sau đây là đúng?
A.
4 3
1
a b
.
B.
3 4
1
a b
.
C.
3 4a b
.
D.
4 3a b
.
Câu 30: Một hình trụ nội tiếp một hình lập phương cạnh a. Thể tích của khối trụ đó là:
Chia sẻ bởi: 
Trịnh Thị Thanh
Trịnh Thị Thanh Liên kết tải về
Link Download chính thức:
Bộ đề thi thử THPT Quốc gia 2020 trường THPT Chuyên Thái Bình Download
Các phiên bản khác và liên quan:
Có thể bạn quan tâm
-
Mẫu 09/ĐK: Đơn đăng ký biến động đất đai
-
Tranh tô màu Pikachu - Bộ tranh tô màu Pikachu đẹp
-
Giáo án Toán lớp 1 (Sách mới) - Giáo án Toán lớp 1 (trọn bộ 5 sách)
-
Tuyển tập đề thi học sinh giỏi môn Toán lớp 3
-
Thuyết minh về Thành Cổ Loa (2 Dàn ý + 5 mẫu)
-
Bộ tranh tô màu chủ đề gia đình cho bé
-
Văn mẫu lớp 10: Phân tích tác phẩm Hiền tài là nguyên khí của quốc gia (2 Dàn ý + 10 Mẫu)
-
Những vần thơ hay - Tuyển tập những bài thơ hay
-
Văn mẫu lớp 9: Nghị luận về hiện tượng học tủ, học vẹt
-
File luyện viết chữ in hoa - Mẫu chữ hoa cho học sinh Tiểu học
Sắp xếp theo
