Bài toán về tạo lập số tự nhiên Chuyên đề bồi dưỡng học sinh giỏi Tiểu học

Bài toán về tạo lập số tự nhiên tổng hợp 3 dạng Toán, kèm theo các ví dụ và hướng dẫn giải chi tiết, giúp các em nắm được quy tắc, dễ dàng tạo lập số tự nhiên, để ôn thi học sinh giỏi và kỳ thi tuyển sinh vào lớp 6 hiệu quả.

Các bài tập về tạo lập số tự nhiên chú ý lập số theo một thứ tự nhất định từ nhỏ đến lớn hoặc ngược lại từ lớn đến nhỏ như thế sẽ ít bị sai sót hơn. Mời các em cùng tham khảo phương pháp giải, ví dụ minh họa và bài tập tự luyện trong bài viết dưới đây:

Bài toán về tạo lập số tự nhiên

Các bài tập về lập số các số tự nhiên thường ta căn cứ vào cấu tạo số tự nhiên để lập các số theo yêu cầu của đề bài. Nên chú ý lập số theo một thứ tự nhất định, như: từ nhỏ đến lớn hoặc ngược lại từ lớn đến nhỏ như thế sẽ ít bị sai sót hơn.

CÁCH 1: Liệt kê

Ví dụ 1: Cho 3 chữ số 1; 2; 3. Lập được tất cả bao nhiêu số tự nhiên có 3 chữ số?

Bài giải:

Các số tự nhiên có 3 chữ số được viết từ 3 chữ số: 1; 2; 3 là:

111; 112; 113; 121; 122; 123; 131; 132; 133

211; 212; 213; 221; 222; 223; 231; 232; 233

311; 312; 313; 321; 322; 323; 331; 332; 333

Có tất cả 27 số.

Ví dụ 2: Cho 3 chữ số 1; 2; 3. Lập được tất cả bao nhiêu số tự nhiên có 3 chữ số khác nhau?

Bài giải:

Các số tự nhiên có 3 chữ số khác nhau được viết từ 3 chữ số: 1; 2; 3 là:

123; 132; 213; 231; 312; 321.

Có tất cả 6 số.

Ví dụ 3: Cho 4 chữ số 0; 1; 2; 3. Lập được tất cả bao nhiêu số tự nhiên có 3 chữ số khác nhau?

Bài giải:

Các số tự nhiên có 3 chữ số khác nhau được viết từ 4 chữ số: 0; 1; 2; 3 là:

102; 103; 120; 123; 130; 132

201; 203; 210; 213; 230; 231

301; 302; 310; 312; 320; 321

Có tất cả 18 số.

CÁCH 2:

Qua 3 ví dụ trên, ta thấy ở bài tập nêu ra có số lượng chữ số cho trước gồm những chữ số cụ thể và yêu cầu của số cần lập là như thế nào? Ta có cách tìm số lượng các số được lập mà không cần phải liệt kê, như sau:

Ví dụ 1: Cho 3 chữ số 1; 2; 3. Lập được tất cả bao nhiêu số tự nhiên có 3 chữ số?

Ở bài tập này đề bài cho ta 3 chữ số là 1; 2; 3. Yêu cầu ta lập các số có 3 chữ số mà số có 3 chữ số gồm có: hàng trăm, hàng chục và hàng đơn vị.

Bài giải:

Với 3 chữ số: 1; 2; 3.

- Hàng trăm có 3 lựa chọn.

- Hàng chục có 3 lựa chọn.

- Hàng đơn vị có 3 lựa chọn.

Số lượng số có 3 chữ số lập được là: 3 x 3 x 3 = 27 (số)

Ví dụ 2: Cho 3 chữ số 1; 2; 3. Lập được tất cả bao nhiêu số tự nhiên có 3 chữ số khác nhau?

Ở bài này khác với bài 1 là lập số có 3 chữ số khác nhau nên nếu đã chọn hàng trăm rồi thì không được chọn ở hàng chục và hàng đơn vị.

Bài giải:

Với 3 chữ số: 1; 2; 3.

- Hàng trăm có 3 lựa chọn.

- Hàng chục có 2 lựa chọn.

- Hàng đơn vị có 1 lựa chọn.

Số lượng số có 3 chữ số lập được là: 3 x 2 x 1 = 6 (số)

Ví dụ 3: Cho 4 chữ số 0; 1; 2; 3. Lập được tất cả bao nhiêu số tự nhiên có 3 chữ số khác nhau?

Ở bài này, các số cho trước có chữ số 0. Chữ số 0 không được đặt ở hàng cao nhất với số tự nhiên (số có 3 chữ số không thể là 023).

Bài giải:

Với 4 chữ số: 0; 1; 2; 3.

- Hàng trăm có 3 lựa chọn. (không được chọn chữ số 0).

- Hàng chục có 3 lựa chọn.

- Hàng đơn vị có 2 lựa chọn.

Số lượng số có 3 chữ số lập được là: 3 x 3 x 2 = 18 (số)

CÁCH 3: Sơ đồ HÌNH CÂY

Lập sơ đồ HÌNH CÂY chính là cụ thể của cách 2 giúp học sinh hiểu và liệt kê ra các số một cách tương đối chính xác hơn, dễ kiểm tra và tránh được những sai sót khi lập số.

Ví dụ 1: Cho 3 chữ số 1; 2; 3. Lập được tất cả bao nhiêu số tự nhiên có 3 chữ số?

Ở bài này ta lập sơ đồ như sau:

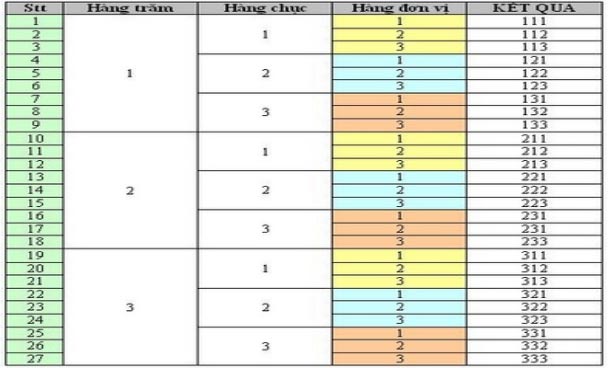
Nhìn qua sơ đồ ta thấy có 3 cách lựa chọn ở hàng trăm (1;2;3), mỗi cách lựa chọn hàng trăm có 3 cách lựa chọn ở hàng chục (1;2;3), mỗi cách lựa chọn hàng chục có 3 cách lựa chọn ở hàng đơn vị (1;2;3).

Như vậy có tất cả: 3 x 3 x 3 = 27 (số)

Ví dụ 2: Cho 3 chữ số 1; 2; 3. Lập được tất cả bao nhiêu số tự nhiên có 3 chữ số khác nhau?

Ta có sơ đồ:

Có tất cả 6 số.

...........

Bài tập vận dụng:

Bài toán 1: Cho 3 chữ số 5, 6, 8. Hãy lập tất cả các số có hai chữ số khác nhau từ 3 chữ số trên. Có tất cả bao nhiêu số như vậy?

Giải: Lần lượt đặt các chữ số 5, 6, 8 vào hàng chục ta được các số sau:

56, 58, 65, 68, 85, 86

Có tất cả 6 số như vậy.

Bài toán 2: Cho 3 chữ số 2, 4, 6.

a. Hãy lập các số có 3 chữ số từ những chữ số trên.

b. Hãy lập các số có 3 chữ số khác nhau từ những số trên.

Giải:

a. Các số được lập phải thỏa mãn các điều kiện:

Có 3 chữ số; được lập từ các chữ số đã cho; trong mỗi số các chữ số có thể lặp lại.

b. Các số được lập phải thỏa mãn các điều kiện:

Có 3 chữ số; được lập từ các chữ số đã cho; trong mỗi số các chữ số không lặp lại.

Bài toán 3: Cho 5 chữ số 1, 2, 3, 4, 5 em viết được bao nhiêu số:

a. Có 3 chữ số

b. Có 3 chữ số khác nhau?

Giải:

a. Có 5 cách chọn chữ số hàng trăm (là một trong năm chữ số 1, 2, 3, 4, 5). Với mỗi cách chọn chữ số hàng trăm thì có 5 cách chọn chữ số hàng chục. Với mỗi cách chọn chữ số hàng chục thì có 5 cách chọn chữ số hàng đơn vị.

Vậy số lượng số có 3 chữ số thỏa mãn bài toán là:

5 x 5 x 5 = 125 (số)

b. Với năm chữ số 1, 2, 3, 4, 5 ta có 5 cách chọn chữ số hàng trăm. Với mỗi cách chọn chữ số ở hàng trăm thì chỉ có 4 cách chọn chữ số ở hàng chục (là một trong bốn chữ số còn lại). Với mỗi cách chọn chữ số ở hàng chục thì chỉ còn 3 cách chọn chữ số ở hàng đơn vị.

Vậy số lượng số có 3 chữ số thỏa mãn bài toán là:

5 x 4 x 3 = 60 (số)

Đáp số: a, 125 số

b, 60 số

Bài toán 4: Cho 5 chữ số 0, 1, 2, 3, 4 em viết được bao nhiêu số có 3 chữ số khác nhau?

Giải: Ta có 4 cách chọn chữ số ở hàng trăm là một trong bốn chữ số khác 0: 1, 2, 3, 4. Sau khi đã chọn chữ số ở hàng trăm ta có 4 cách chọn chữ số ở hàng chục là một trong bốn chữ số còn lại. sau khi đã chọn chữ số ở hàng trăm, hàng chục rồi thì chỉ còn 3 cách chọn chữ số ở hàng đơn vị.

Vậy số lượng số có 3 chữ số thỏa mãn bài toán là:

4 x 4 x 3 = 48 (số)

Đáp số: 48 số

..................................