100 đề thi học sinh giỏi môn Toán lớp 5 (Có đáp án) Đề thi học sinh giỏi lớp 5 môn Toán

Bộ đề thi học sinh giỏi môn Toán lớp 5 gồm 100 đề thi, có đáp án kèm theo, giúp các em học sinh lớp 5 nắm chắc các dạng bài tập thường gặp trong đề thi học sinh giỏi, để ôn thi hiệu quả, đạt kết quả cao trong kỳ thi học sinh giỏi năm 2023 - 2024.

Với 100 Đề thi HSG môn Toán 5 có đáp án, còn giúp thầy cô tham khảo để giao đề luyện tập cho học sinh của mình ở nhà, giúp các em nắm thật chắc kiến thức Toán 5 nâng cao. Mời thầy cô và các em cùng theo dõi bài viết dưới đây của Eballsviet.com:

Đề thi học sinh giỏi môn Toán lớp 5 - Đề 1

Bài 1 (3 điểm): Tổng của ba số tự nhiên là 117. Biết rằng số thứ hai lớn hơn số thứ nhất là 5 đơn vị và nhỏ hơn số thứ ba 5 đơn vị. Tìm ba số đó?

Bài 2 (3 điểm): Hòa đố Bình: "Ngày 22 tháng 12 năm 2008 là ngày thứ hai. Cậu có biết ngày 22 tháng 12 năm 1944 là ngày thứ mấy không?". Bình nghĩ một lúc rồi lắc đầu chịu thua. Em có tính giúp Bình được không?

Bài 3 (3 điểm): Tìm số có ba chữ số, biết số đó chia cho 2 dư 1, chia cho 5 dư 3 và chia hết cho 3, biết chữ số hàng trăm là 8.

Bài 4 (3 điểm): Thầy giáo ra cho hai bạn một lượng bài toán bằng nhau. Sau vài ngày, bạn thứ nhất làm được 20 bài, bạn thứ hai làm được 22 bài. Như vậy số bài tập thầy giáo ra cho mỗi bạn nhiều gấp 4 lần số bài toán của cả hai bạn chưa làm xong. Hỏi thầy giáo ra cho mỗi bạn bao nhiêu bài toán?

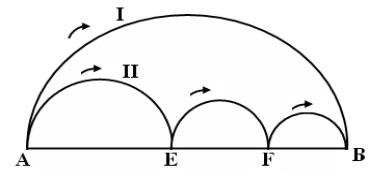
Bài 5 (3 điểm): Hai chú kiến có vận tốc như nhau cùng xuất phát một lúc từ A và bò đến B theo hai đường cong I và II (như hình vẽ bên). Hỏi chú kiến nào bò về đích trước?

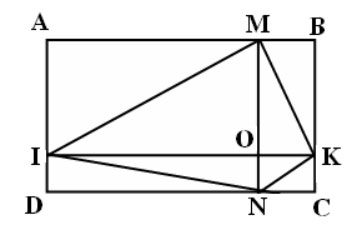
Bài 6 (5 điểm): Mảnh vườn hình chữ nhật ABCD được ngăn thành bốn mảnh hình chữ nhật nhỏ (như hình vẽ). Biết diện tích các mảnh hình chữ nhật MBKO, KONC và OIDN lần lượt là: 18 cm2; 9 cm2 và 36 cm2. a) Tính diện tích mảnh vườn hình chữ nhật ABCD. b) Tính diện tích mảnh vườn hình tứ giác MKNI.

ĐÁP ÁN

Bài 1: (3 điểm): Coi số thứ nhất là 1 phần, theo đề bài ta có sơ đồ: (0,5 đ)

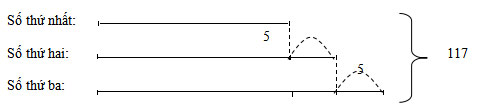
Theo sơ đồ ta có: (0,5 đ)

Mỗi phần bằng nhau là: (117 – 5- 5- 5 ): 3= 34

Số thứ nhất là 34 (0,5đ)

Số thứ hai là: 34 + 5= 39 (0,5đ)

Số thứ ba là: 39 + 5 = 44 (0,5đ)

Đáp số: Số thứ nhất: 34 ;Số thứ hai: 39; Số thứ ba: 44 (0,5 đ)

Bài 2. (3 điểm):

Từ năm 1944 đến năm 2008 tròn 64 năm. Do năm 1944 và 2008 đều là các năm nhuận, nên từ năm 1944 đến năm 2008 có: (2008 - 1944) : 4 + 1 = 17 (năm nhuận) (1 đ).

Kể từ sau ngày 22 tháng 12 năm 1944 đến ngày 22 tháng 12 năm 2008 có 16 ngày 29 tháng 2. Do đó số ngày sau ngày 22 tháng 12 năm 1944 đến ngày 22 tháng 12 năm 2008 là: 365 x 64 + 16 = 23376 (ngày). (1 đ)

Vì 23376 : 7 = 3339 (dư 3) nên suy ra ngày 22 tháng 12 năm 1944 là ngày thứ sáu.

Bài 3. (3 điểm):

Theo đề bài ta có: số đó có dạng \(\overline{8ab}\), 0 ≤ a; b ≤ 9; a ≠ 0 (0,25đ)

Để \(\overline{8ab}\) chia 2 dư 1 thì b = 1;3;5;7;9 (1) (0,25đ)

Để \(\overline{8ab}\) chia 5 dư 3 thì b = 3 hoặc 8 (2) (0,25đ)

Từ (1) và (2) suy ra b = 3 (0,25đ)

Số đó có dạng \(\overline{8a3}\) (0,5đ)

Để \(\overline{8a3}\) chia hết cho 3 thì (8 +a + 3) chia hết cho 3 hay (11 + a) chia hết cho 3 (0,5đ)

Suy ra a = 1; 4; 7 (0,5đ)

Vậy các số cần tìm là: 813; 843; 873 (0,5đ)

Bài 4. (3 điểm):

Số bài tập của 2 bạn còn lại đúng bằng \(\frac{1}{4}\)số bài tập thầy giáo ra cho mỗi bạn, vậy số bài tập của 2 bạn còn lại đúng bằng \(\frac{1}{8}\)tổng số bài tập thầy ra cho 2 bạn. (0,75 đ)

Vậy \(\frac{7}{8}\) số bài tập thầy ra cho 2 bạn đúng bằng : 22 + 20 = 42 (bài tập). (0,75 đ)

Tổng số bài tập thầy ra cho 2 bạn là: \(42x\frac{8}{7}=48\) (bài tập). (0,75 đ)

Số bài tập thầy ra cho mỗi bạn là: 48 : 2 = 24 (bài tập). (0,75 đ)

Bài 5. (3 điểm):

Chú kiến bò từ A đến B theo đường cong II đi được quãng đường là:

\(\frac{AEx3,14}{2}+\frac{EFx3,14}{2}+\frac{FBx3,14}{2}=\frac{3,14}{2}x(AE+EF+FB)=\frac{3,14}{2}xAB\). (1 đ)

Chú kiến bò theo đường cong I đi được quãng đường bằng: \(\frac{3,14}{2}xAB\) (1 đ)

Vậy hai chú kiến đến B cùng một lúc. (1 đ)

Bài 6. (5 điểm):

a) (2,5 điểm).Tỉ số diện tích của hình chữ nhật IOND và OKCN là: 36 : 9 = 4 (lần). (0,5đ)

Hình chữ nhật IOND và OKCN có chung cạnh ON do đó IO = OK x 4. (0,5đ)

Hình chữ nhật AMOI và MBKO có chung cạnh MO, mà độ dài cạnh IO = OK x 4. Do đó diện tích hình chữ nhật AMOI bằng 4 lần diện tích hình chữ nhật MBKO. (0,5đ)

Diện tích hình chữ nhật AMOI là: 18 x 4 = 72 (cm²). (0,5đ)

Diện tích hình chữ nhật ABCD là: 72 + 18 + 9 + 36 = 135 (cm²). (0,5đ)

b) (2,5 điểm).Diện tích hình tam giác MOI là: 72 : 2 = 36 (cm²). (0,5đ)

Diện tích hình tam giác MOK là: 18 : 2 = 9 (cm²). (0,5đ) Diện tích hình tam giác OKN là: 9 : 2 = 4,5 (cm²). (0,5đ)

Diện tích hình tam giác OIN là: 36 : 2 = 18 (cm²). (0,5đ)

Diện tích hình tứ giác MKNI là: 36 + 9 + 4,5 + 18 = 67,5 (cm²). (0,5đ)

(Học sinh giải theo cách khác đúng vẫn cho điểm tối đa)

Đề thi học sinh giỏi môn Toán lớp 5 - Đề 2

Bài 1: (3 điểm) Tìm tất cả các số tự nhiên có 2 chữ số vừa chia hết cho 2 vừa chia hết cho 3 lại vừa chia hết cho 5?

Bài 2: (3 điểm) Lúc 6 giờ một xe máy đi từ tỉnh A đến tỉnh B với vận tốc 45km/giờ. Lúc 6 giờ 20 phút cùng ngày một ôtô cũng đi từ tỉnh A đến tỉnh B với vận tốc 55 km/giờ. Hỏi ôtô đuổi kịp xe máy lúc mấy giờ ? Địa điểm gặp nhau cách tỉnh B bao nhiêu kilômet? Biết quãng đường từ tỉnh A đến tỉnh B dài 165km.

Bài 3: (3 điểm) Bạn Khoa đến cửa hàng bán sách cũ và mua được một quyển sách Toán rất hay gồm 200 trang. Về đến nhà đem sách ra xem. Khoa mới phát hiện ra từ trang 100 đến trang 125 đã bị xé. Hỏi cuốn sách này còn lại bao nhiêu trang?

Bài 4: (3 điểm) Tìm một số có hai chữ số, biết rằng nếu viết thêm vào bên trái số đó một chữ số 3 thì ta được số mới mà tổng số đã cho và số mới bằng 414.

Bài 5: (3 điểm)

Cuối học kỳ một, bài kiểm tra môn Toán của lớp 5A có số học sinh đạt điểm giỏi bằng \(\frac{3}{7}\)số học sinh còn lại của lớp. Giữa học kỳ hai, bài kiểm tra môn Toán của lớp có thêm 3 học sinh đạt điểm giỏi, nên số học sinh đạt điểm giỏi của cả lớp bằng \(\frac{2}{3}\)số học sinh còn lại của lớp. Hỏi giữa học kỳ hai bài kiểm tra môn Toán của lớp 5A có bao nhiêu học sinh đạt điểm giỏi ? Biết rằng số học sinh lớp 5A không đổi.

Bài 6: (5 điểm)

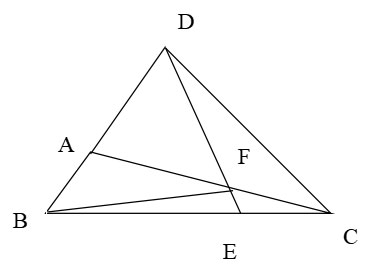
Cho tam giác ABC; E là một điểm trên BC sao cho BE = 3EC; F là một điểm trên AC sao cho AF = 2FC; EF cắt BA kéo dài tại D. Biết diện tích hình tam giác CEF bằng 2cm².

1) Tính diện tích hình tam giác ABC.

2) So sánh diện tích hai hình tam giác BDF và CDF.

3) So sánh DF với FE.

ĐÁP ÁN

Bài 1: (3 điểm)

• Đặt điều kiện một số tự nhiên có 2 chữ số vừa chia hết cho 2 và vừa chia hết cho 5 là số có tận cùng là 0, vậy số đó là số tròn chục. (1đ)
• Để các số tròn chục chia hết cho 3 thì chữ số hàng chục phải chia hết cho 3(1đ) Vậy các số đó là: 30; 60 ; 90. ( 1đ)

Bài 2: (3 điểm)

Bài 3. (3 điểm):

Trang 100 bị xé nên trang 99 cũng bị xé ( vì hai trang này nằm trên một tờ giấy). Trang 125 bị xé nên trang 126 cũng bị xé (vì hai trang này nằm trên một tờ giấy). (1 đ)

Số trang sách bị xé mất là: 126 - 99 + 1 = 28 (trang). (1 đ)

Số trang còn lại của quyển sách là: 200 - 28 = 172 (trang). (1 đ)

Bài 4: (3 điểm):

Gọi số phải tìm là \(\overline{ab}\), nếu viết thêm chữ số 3 vào bên phải số đó ta được số mới \(\overline{3ab}\). (0,5 đ)

Theo đề bài ta có: \(\overline{ab}\) + \(\overline{3ab}\) = 414 (0,5 đ)

\(\overline{ab}\) + 300 + \(\overline{ab}\) = 414 (0,5 đ)

2 x \(\overline{ab}\) = 414 - 300 (0,5 đ)

2 x \(\overline{ab}\) = 114 (0,5 đ)

\(\overline{ab}\) = 114 : 2 (0,25 đ)

\(\overline{ab}\) = 57 (0,25 đ)

Bài 5 (3 điểm)

Bài giải

Bài 6. (5 điểm) Hình vẽ đúng 0,25 đ

.....

>> Tải file để tham khảo các mẫu còn lại!