Tìm điều kiện tham số m để ba đường thẳng đồng quy Ôn tập Toán 9
Tìm m để 3 đường thẳng đồng quy là một trong những bài toán cơ bản trong chương trình lớp 9 hiện hành và thường xuất hiện trong các bài thi vào 10 môn Toán.
Cách tìm m để ba đường thẳng đồng quy tổng hợp kiến thức về lý thuyết, cách tìm, ví dụ minh họa, các dạng bài tập tự luyện kèm theo. Qua đó giúp các bạn học sinh tham khảo, hệ thống lại kiến thức để giải nhanh các bài tập đường thẳng đồng quy. Ngoài ra để nâng cao kiến thức môn Toán thật tốt các em xem thêm một số tài liệu như: tìm giá trị x để A nhận giá trị nguyên, chuyên đề Giải phương trình bậc 2 chứa tham số, bài tập hệ thức Vi-et và các ứng dụng.
Tìm m để 3 đường thẳng đồng quy
I. Ba đường thẳng đồng quy là gì?
Cho ba đường thẳng a, b, c không trùng nhau. Khi đó ta nói ba đường thẳng a, b, c đồng quy khi ba đường thẳng đó cùng đi qua một điểm O nào đó.
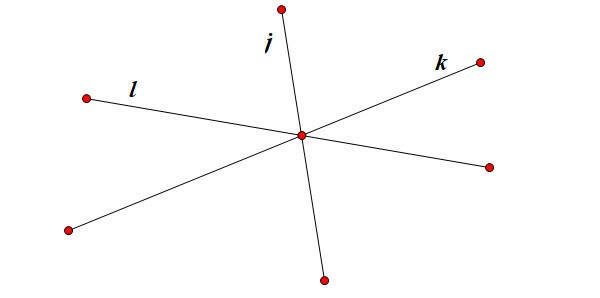
II. Cách tìm m để 3 đường thẳng đồng quy
Các bước giải toán như sau:
Bước 1: Tìm điều kiện để các đường thẳng cắt nhau, để đường thẳng là hàm số bậc nhất (nếu có)
Bước 2: Tìm giao điểm của hai đường thẳng (hai đường thẳng không chứa m) để 3 đường thẳng đồng quy thì giao điểm đó phải thỏa mãn khi thay vào đường thẳng còn lại. Từ đó suy ra giá trị tham số m.
Bước 3: Kết luận giá trị của m.
III. Ví dụ tìm m để 3 đường thẳng đồng quy
Ví dụ 1: Cho ba đường thẳng y = 2x + 1 (d1); y = x – 1 (d2) và u = (m + 1)x – 2. Tìm điều kiện của tham số m để ba đường thẳng đồng quy.
Gợi ý đáp án
Hoành độ giao điểm của d1 và d2 là nghiệm của phương trình:
2x + 1 = x – 1
=> x = -2
Với x = -2 => y = -2 – 1 = -3
Suy ra hai đường thẳng d1 và d2 cắt nhau tại điểm A(-2; -3)
Để ba đường thẳng đồng quy thì điểm A(-2; -3) thuộc đồ thị hàm số y = (m + 1)x – 2. Khi đó ta có:
-3 = (m + 1).(-2) – 2
=> ![]() \(m = - \frac{1}{2}\)
\(m = - \frac{1}{2}\)
Vậy với ![]() \(m = - \frac{1}{2}\) thì ba đường thẳng đã cho đồng quy.
\(m = - \frac{1}{2}\) thì ba đường thẳng đã cho đồng quy.
Ví dụ 2: Tìm tham số m để ba đường thẳng y = x – 2; y = 2x + m + 1 và y = 3x – 2 cắt nhau tại một điểm.
Gợi ý đáp án
Hoành độ giao điểm của y = x - 2 và y = 3x - 2 là nghiệm của phương trình:
x – 2 = 3x – 2
=> x = 0
Với x = 0 => y = 0 – 2 = -2
Suy ra hai đường thẳng y = x - 2 và y = 3x - 2 cắt nhau tại điểm B(0; -2)
Để ba đường thẳng đồng quy thì điểm B(0; -2) thuộc đồ thị hàm số y = 2x + m + 1. Khi đó ta có:
0 = 2.(-2) + m + 1
=> m – 3 = 0
=> m = 3
Vậy với m = 3 thì ba đường thẳng đã cho đồng quy.
Ví dụ 3: Tìm m để 3 đường thẳng đồng quy:
(d1): x + y - 2 = 0
(d2): 2x + 3y = 0
(d3): mx + y =2
Gợi ý đáp án
Gọi A là giao điểm của d1 và d2. Khi đó A thỏa mã hệ phương trình:
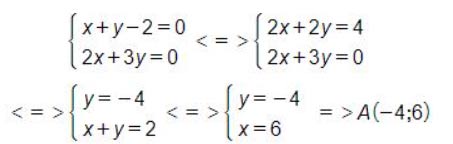
Để 3 đường thẳng đồng quy thì d3 phải đi qua điểm A:
=> -4m + 6 = 2
=> m = 1.
Vậy, với m = 1 thì 3 đường thẳng đã cho đồng quy.
IV. Bài tập tìm m để ba đường thẳng đồng quy
Bài tập 1: Cho ba đường thẳng y = x + 6 (d1); y = 3x + 7 (d2) và y = (2 – m)x + 1 (d3). Tìm m để (d1), (d2) và (d3) đồng quy.
Bài tập 2: Cho đường thẳng (d1): y = 2x + 1, (d2) y = 3, (d3): y = kx + 5
a) Xác định tọa độ giao điểm A của 2 đường thẳng d1 và d2
b) Tìm m để ba đường thẳng trên đồng quy.
Bài tập 3: Cho các đường thẳng (d1): y = x + 2, (d2): y = - 2x + 5, (d3): y = 3x, (d): y = mx + m - 5 trong cùng hệ trục tọa độ.
a, Chứng minh (d1); (d2); (d3) đồng quy.
b, Tìm m để (d1); (d2); (d3) và (d) đồng quy.
Bài tập 4: Cho ba đường thẳng:
d1: y = x + 2
d2: y = 2x + 1
d3: y = (m2 + 1)x + m
Tính các giá trị của m để ba đường thẳng cắt nhau tại một điểm.
Bài tập 5: Tìm m để đồ thị của các hàm số y = - x + 2; y = 2x - 1; y = (m - 2)x + m - 1 đồng quy.
Bài tập 6: Tìm m để đồ thị của các hàm số y = 2x + 3; y = x và y = - 4mx + 9 cắt nhau tại một điểm.
Bài tập 7: Cho ba đường thẳng y = 2x + 1 (d1); y = x – 1 (d2) và (d3): u = (m + 1)x – 2. Tìm điều kiện của tham số m để ba đường thẳng đồng quy.
Bài tập 8: Tìm tham số m để ba đường thẳng y = x - 2; y = 2x + m + 1 và y = 3x - 2 cắt nhau tại một điểm.
Bài tập 9 Cho 3 đường thẳng d1: y = - 2x, d2; y = 1,5x + 7 và d3: y = - 2mx + 5
a) Tìm tọa độ giao điểm hai đường thẳng d1, d2
b) Tìm các giá trị của tham số m để ba đường thẳng d1, d2, d3 đồng quy.
Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:












 Đề thi giữa kì 2 lớp 9
Đề thi giữa kì 2 lớp 9
 Đề thi học kì 2 Lớp 9
Đề thi học kì 2 Lớp 9
 Đề thi giữa kì 1 lớp 9
Đề thi giữa kì 1 lớp 9
 Đề thi học kì 1 Lớp 9
Đề thi học kì 1 Lớp 9
 Toán 9
Toán 9
 Toán 9 Kết nối tri thức
Toán 9 Kết nối tri thức
 Toán 9 Cánh Diều
Toán 9 Cánh Diều
 Toán 9 Chân trời sáng tạo
Toán 9 Chân trời sáng tạo
 Văn 9 Kết nối tri thức
Văn 9 Kết nối tri thức