Tập nghiệm của bất phương trình Tìm tập nghiệm của bất phương trình
Tìm tập nghiệm của bất phương trình là dạng bài tập khó trong chương trình Toán lớp 10 và nhiều bạn học sinh chưa biết cách tìm tập nghiệm như thế nào.
Chính vì thế trong bài viết dưới đây Eballsviet.com giới thiệu đến các bạn toàn bộ kiến thức lý thuyết và một số bài tập kèm theo ví dụ minh họa về cách tìm tập nghiệm. Hi vọng qua tài liệu này các bạn có thêm nhiều nguồn ôn tập, củng cố kiến thức để nhanh chóng biết giải các bài toán về tập nghiệm của bất phương trình. Bên cạnh đó các bạn xem thêm một số tài liệu khác như: tóm tắt kiến thức và phương pháp giải Toán lớp 10, tìm m để phương trình vô nghiệm, Các dạng bài tập toán về mệnh đề và tập hợp, tập nghiệm của bất phương trình,
Tập nghiệm của bất phương trình
1. Bất phương trình là gì?
- Khác với phương trình, bất phương trình có hai vế không bằng nhau, có thể lớn hơn hoặc nhỏ hơn. Nghiệm của bất phương trình không phải chỉ là một giá trị mà sẽ bao gồm cả một tập hợp giá trị thỏa mãn điều kiện của bất phương trình.
- Có rất nhiều dạng bất phương trình khác nhau như: bất phương trình bậc một, bất phương trình bậc hai, bất phương trình vô tỷ, bất phương trình chứa căn, bất phương trình logarit. Mỗi dạng bài lại có một cách giải bất phương trình khác nhau, tùy theo đặc điểm của bất phương trình.
2. Tập nghiệm S của bất phương trình là gì?
Trước hết ta xét đến định nghĩa bất phương trình một ẩn
- Bất phương trình một ẩn là một mệnh đề chứa biến x so sánh hai hàm số f(x) và g(x) trên trường số thực dưới một trong các dạng
f(x) < g(x), f(x) > g(x); f(x) ≥ g(x); f(x) ≤ g(x)
- Giao của hai tập xác định của các hàm số f(x) và g(x) được gọi là tập xác định của bất phương trình.
- Nếu với giá trị x =a, f(a) > 0 là bất đẳng thức đúng thì ta nói rằng a nghiệm đúng bất phương trình f(x) > 0, hay a là nghiệm của bất phương trình.
Tập hợp tất cả các nghiệm của bất phương trình được gọi là tập nghiệm hay lời giải của bất phương trình, đôi khi nó cũng được gọi là miền đúng của bất phương trình. Trong nhiều tài liệu người ta cũng gọi tập nghiệm của bất phương trình là nghiệm của bất phương trình.
Ví dụ Bất phương trình 4.x + 2 > 0 nghiệm đúng với mọi số thực x > -0.5. Tập nghiệm của bất phương trình là { x ∈ R | x > -0.5 } = (0.5; ![]() \(\infty\))
\(\infty\))
Phân loại bất phương trình:
- Các bất phương trình đại số bậc k là các bất phương trình trong đó f(x) là đa thức bậc k.
- Các bất phương trình vô tỷ là các bất phương trình có chứa phép khai căn
- Các bất phương trình mũ là các bất phương trình có chứa hàm mũ (chứa biến trên lũy thừa.
- Các bất phương trình logarit là các bất phương trình có chứa hàm logarit (chứa biến trong dấu logarit).
3. Lưu ý khi giải bất phương trình?
- Lưu ý khi giải bất phương trình bậc nhất một ẩn
Bất phương trình bậc nhất một ẩn ax + b >0 là dạng tổng quát để hướng dẫn học sinh giải toán. Đầu tiên, các em tìm ra nghiệm của bất phương trình, sau đó hướng dẫn các em biểu diễn trên trục số kết quả tìm được và đưa vào tập nghiệm của bất phương trình. Bất phương trình bậc nhất một ẩn khá dễ chinh phục, các gia sư cũng cần đưa ra những bài mẹo, những bài có kết quả vô nghiệm để kích thích tính tư duy sáng tạo trong toán học của các em. Lưu ý điều kiện trước khi giải bất kỳ bài toán nào nhé.
- Lưu ý khi giải bất phương trình tích
Bất phương trình dạng này khá phức tạp, tất nhiên trước tiên các em cần sử dụng các phép biến đổi để đưa các bất phương trình về dạng bất phương trình tích. Tìm tất cả các nghiệm của mỗi phương trình bậc nhất nhỏ trong tích, sau đó xét dấu bằng bảng biến thiên. Tìm nghiệm tùy vào dấu của bất phương trình, nếu bất phương trình là <0 thì chọn giá trị x tại những ô f(x) mang giá trị âm và ngược lại. Học sinh cần làm tốt việc giải bất phương trình bật nhất một ẩn thành thạo và có thể sử dụng tốt các kiến thức bổ trợ mới có thể làm tốt bài tập này.
4. Bài tập tìm tập nghiệm của bất phương trình
Bài tập 1: Tìm tập nghiệm S của bất phương trình ![]() \(\sqrt {{x^2} - 5x - 6} + 2{x^2} > 10x + 15\)
\(\sqrt {{x^2} - 5x - 6} + 2{x^2} > 10x + 15\)
Gợi ý đáp án
Điều kiện xác định: ![]() \({x^2} - 5x - 6 \geqslant 0 \Leftrightarrow x \in \left( { - \infty ; - 1} \right] \cup \left[ {6; + \infty } \right)\)
\({x^2} - 5x - 6 \geqslant 0 \Leftrightarrow x \in \left( { - \infty ; - 1} \right] \cup \left[ {6; + \infty } \right)\)
Bất phương trình tương đương: \(\begin{matrix}
\sqrt {{x^2} - 5x - 6} + 2{x^2} > 10x + 15 \hfill \\
\Leftrightarrow \sqrt {{x^2} - 5x - 6} > - 2{x^2} + 10x + 15 \hfill \\
\Leftrightarrow \sqrt {{x^2} - 5x - 6} > - 2\left( {{x^2} - 5x - 6} \right) + 3\left( * \right) \hfill \\
\end{matrix}\)
\(\begin{matrix}
\sqrt {{x^2} - 5x - 6} + 2{x^2} > 10x + 15 \hfill \\
\Leftrightarrow \sqrt {{x^2} - 5x - 6} > - 2{x^2} + 10x + 15 \hfill \\
\Leftrightarrow \sqrt {{x^2} - 5x - 6} > - 2\left( {{x^2} - 5x - 6} \right) + 3\left( * \right) \hfill \\
\end{matrix}\)
Đặt ![]() \(\sqrt {{x^2} - 5x - 6} = t;\left( {t \geqslant 0} \right)\) (**)
\(\sqrt {{x^2} - 5x - 6} = t;\left( {t \geqslant 0} \right)\) (**)
![\begin{matrix}
\left( * \right) \Leftrightarrow t > - 2{t^2} + 3 \hfill \\
\Leftrightarrow 2{t^2} + t - 3 > 0 \hfill \\
\Leftrightarrow t \in \left( { - \infty ; - \dfrac{3}{2}} \right] \cup \left[ {1; + \infty } \right) \hfill \\
\end{matrix}](https://st.download.vn/data/image/blank.png) \(\begin{matrix}
\left( * \right) \Leftrightarrow t > - 2{t^2} + 3 \hfill \\
\Leftrightarrow 2{t^2} + t - 3 > 0 \hfill \\
\Leftrightarrow t \in \left( { - \infty ; - \dfrac{3}{2}} \right] \cup \left[ {1; + \infty } \right) \hfill \\
\end{matrix}\)
\(\begin{matrix}
\left( * \right) \Leftrightarrow t > - 2{t^2} + 3 \hfill \\
\Leftrightarrow 2{t^2} + t - 3 > 0 \hfill \\
\Leftrightarrow t \in \left( { - \infty ; - \dfrac{3}{2}} \right] \cup \left[ {1; + \infty } \right) \hfill \\
\end{matrix}\)
Kết hợp với điều kiện (**) ![]() \(\Rightarrow t \in \left[ {1; + \infty } \right)\)
\(\Rightarrow t \in \left[ {1; + \infty } \right)\)
![\begin{matrix}
\Rightarrow \sqrt {{x^2} - 5x - 6} \geqslant 1 \Leftrightarrow {x^2} - 5x - 6 \geqslant 1 \hfill \\
\Rightarrow x \in \left( { - \infty ;\dfrac{{5 - \sqrt {53} }}{2}} \right] \cup \left[ {\dfrac{{5 + \sqrt {53} }}{2}; + \infty } \right) \hfill \\
\end{matrix}](https://st.download.vn/data/image/blank.png) \(\begin{matrix}
\Rightarrow \sqrt {{x^2} - 5x - 6} \geqslant 1 \Leftrightarrow {x^2} - 5x - 6 \geqslant 1 \hfill \\
\Rightarrow x \in \left( { - \infty ;\dfrac{{5 - \sqrt {53} }}{2}} \right] \cup \left[ {\dfrac{{5 + \sqrt {53} }}{2}; + \infty } \right) \hfill \\
\end{matrix}\)
\(\begin{matrix}
\Rightarrow \sqrt {{x^2} - 5x - 6} \geqslant 1 \Leftrightarrow {x^2} - 5x - 6 \geqslant 1 \hfill \\
\Rightarrow x \in \left( { - \infty ;\dfrac{{5 - \sqrt {53} }}{2}} \right] \cup \left[ {\dfrac{{5 + \sqrt {53} }}{2}; + \infty } \right) \hfill \\
\end{matrix}\)
Vậy tập nghiệm của bất phương trình là ![x \in \left( { - \infty ;\frac{{5 - \sqrt {53} }}{2}} \right] \cup \left[ {\frac{{5 + \sqrt {53} }}{2}; + \infty } \right)](https://st.download.vn/data/image/blank.png) \(x \in \left( { - \infty ;\frac{{5 - \sqrt {53} }}{2}} \right] \cup \left[ {\frac{{5 + \sqrt {53} }}{2}; + \infty } \right)\)
\(x \in \left( { - \infty ;\frac{{5 - \sqrt {53} }}{2}} \right] \cup \left[ {\frac{{5 + \sqrt {53} }}{2}; + \infty } \right)\)
Bài tập 2: Tìm tập nghiệm của bất phương trình: ![]() \(\frac{{{x^2} - 4}}{{{x^2} - 6x + 8}} \leqslant 0\)
\(\frac{{{x^2} - 4}}{{{x^2} - 6x + 8}} \leqslant 0\)
Gợi ý đáp án
Điều kiện xác định x2 – 6x + 8 ≠ 0 ⟺ x ≠ 2, x ≠ 4
![]() \(\frac{{{x^2} - 4}}{{{x^2} - 6x + 8}} \leqslant 0 \Leftrightarrow \frac{{\left( {x - 2} \right)\left( {x + 2} \right)}}{{\left( {x - 4} \right)\left( {x - 2} \right)}} \leqslant 0 \Leftrightarrow \frac{{x + 2}}{{x - 4}} \leqslant 0\)
\(\frac{{{x^2} - 4}}{{{x^2} - 6x + 8}} \leqslant 0 \Leftrightarrow \frac{{\left( {x - 2} \right)\left( {x + 2} \right)}}{{\left( {x - 4} \right)\left( {x - 2} \right)}} \leqslant 0 \Leftrightarrow \frac{{x + 2}}{{x - 4}} \leqslant 0\)
Lập bảng xét dấu ta có:
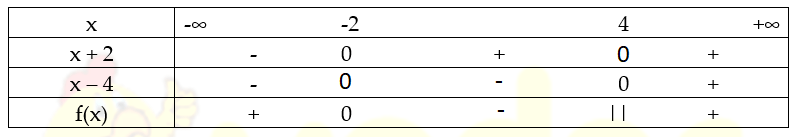
Từ bảng xét dấu ta kết luận: Tập nghiệm của bất phương trình là: x ∈ [ -2 ; 4)
Bài tập 3: Giải bất phương trình: (x2 + 3x + 1)(x2 + 3x – 3) ≥ 5 (*)
Gợi ý đáp án
Tập xác định D = ![]() \(\mathbb{R}\)
\(\mathbb{R}\)
Đặt x2 + 3x – 3 = t ⟹ x2 + 3x + 1 = t + 4
Bất phương trình (*) ⟺ t(t+4) ≥ 5
⟺ t2 + 4t – 5 ≥ 0
⟺ t ∈ ( -∞ ; -5] ∪ [1; +∞ )
![\begin{matrix}
\Rightarrow \left[ {\begin{array}{*{20}{c}}
{{x^2} + 3x - 3 \leqslant - 5} \\
{{x^2} + 3x - 3 \geqslant 1}
\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}
{{x^2} + 3x + 2 \leqslant 0} \\
{{x^2} + 3x - 4 \geqslant 0}
\end{array}} \right. \hfill \\
\Leftrightarrow \left[ {\begin{array}{*{20}{c}}
{x \in \left[ { - 2; - 1} \right]} \\
{x \in \left( { - \infty - 4} \right] \cup \left[ {1; + \infty } \right)}
\end{array}} \right. \Rightarrow x \in \left( { - \infty - 4} \right] \cup \left[ {1; + \infty } \right) \hfill \\
\end{matrix}](https://st.download.vn/data/image/blank.png) \(\begin{matrix}
\Rightarrow \left[ {\begin{array}{*{20}{c}}
{{x^2} + 3x - 3 \leqslant - 5} \\
{{x^2} + 3x - 3 \geqslant 1}
\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}
{{x^2} + 3x + 2 \leqslant 0} \\
{{x^2} + 3x - 4 \geqslant 0}
\end{array}} \right. \hfill \\
\Leftrightarrow \left[ {\begin{array}{*{20}{c}}
{x \in \left[ { - 2; - 1} \right]} \\
{x \in \left( { - \infty - 4} \right] \cup \left[ {1; + \infty } \right)}
\end{array}} \right. \Rightarrow x \in \left( { - \infty - 4} \right] \cup \left[ {1; + \infty } \right) \hfill \\
\end{matrix}\)
\(\begin{matrix}
\Rightarrow \left[ {\begin{array}{*{20}{c}}
{{x^2} + 3x - 3 \leqslant - 5} \\
{{x^2} + 3x - 3 \geqslant 1}
\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}
{{x^2} + 3x + 2 \leqslant 0} \\
{{x^2} + 3x - 4 \geqslant 0}
\end{array}} \right. \hfill \\
\Leftrightarrow \left[ {\begin{array}{*{20}{c}}
{x \in \left[ { - 2; - 1} \right]} \\
{x \in \left( { - \infty - 4} \right] \cup \left[ {1; + \infty } \right)}
\end{array}} \right. \Rightarrow x \in \left( { - \infty - 4} \right] \cup \left[ {1; + \infty } \right) \hfill \\
\end{matrix}\)
Vậy tập nghiệm của bất phương trình là x ∈ ( -∞ ; -4] ∪ [1; +∞ )
5. Bài tập tự luyện tìm tập nghiệm của bpt
Câu 1: Tìm tập nghiệm S của bất phương trình x2- 4 > 0
| A. S = (-2 ; 2). | B. S = (-∞ ; -2) ∪ (2; +∞) |
| C. S = (-∞ ; -2] ∪ [2; +∞) | D. S = (-∞ ; 0) ∪ (4; +∞) |
Câu 2: Tìm tập nghiệm S của bất phương trình x2 – 4x + 4 > 0.
| A. S = R | B. S = R\{2} |
| C. S = (2; ∞) | D. S =R\{-2} |
Câu 3: Tập nghiệm S = (-4; 5) là tập nghiệm của bất phương trình nào sau đây?
| A. (x + 4)(x + 5) < 0 | B. (x + 4)(5x - 25) ≥ 0 |
| C. (x + 4)(x + 25) < 0 | D. (x - 4)(x - 5) < 0 |
Câu 4: Cho biểu thức: f(x) = ax2 + bx + c (a ≠ 0) và ∆ = b2 – 4ac. Chọn khẳng định đúng trong các khẳng định dưới đây?
A. Khi ∆ < 0 thì f(x) cùng dấu với hệ số a với mọi x ∈ ![]() \(\mathbb{R}\).
\(\mathbb{R}\).
B. Khi ∆ = 0 thì f(x) trái dấu với hệ số a với mọi ![]() \(x \ne \frac{{ - b}}{{2a}}\).
\(x \ne \frac{{ - b}}{{2a}}\).
C. Khi ∆ < 0 thì f(x) cùng dấu với hệ số a với mọi ![]() \(x \ne \frac{{ - b}}{{2a}}\).
\(x \ne \frac{{ - b}}{{2a}}\).
D. Khi ∆ > 0 thì f(x) trái dấu với hệ số a với mọi x ∈ ![]() \(\mathbb{R}\).
\(\mathbb{R}\).
Câu 5: Tìm tập nghiệm của bất phương trình: -x2 + 2017x + 2018 > 0
| A. S = [-1 ; 2018] | B. S = (-∞ ; -1) ∪ (2018; +∞) |
| C. S = (-∞ ; -1] ∪ [2018; +∞) | D. S = (-1 ; 2018) |
Câu 6: Giải các bất phương trình sau:
| a. |
b. |
| c. |
d. |
Câu 7: Tìm tập nghiệm của các bất phương trình sau:
| a. |
b. |
| c. |
d. |
| e. |
f. |
Câu 8: Tập nghiệm S của bất phương trình 5x-1 = ≥ 5x/2 +3 là:
A. S = (+![]() \(\infty\); 5)
\(\infty\); 5)
B. S = (-![]() \(\infty\);2)
\(\infty\);2)
C. S = (-5/2; +![]() \(\infty\))
\(\infty\))
D. S = (20/23; + ![]() \(\infty\))
\(\infty\))
Câu 9: Bất phương trình ![]() \(\frac{3x+5}2-1\leq\frac{x+2}3+x\) có bao nhiêu nghiệm nguyên lớn hơn -10
\(\frac{3x+5}2-1\leq\frac{x+2}3+x\) có bao nhiêu nghiệm nguyên lớn hơn -10
A. 4
B. 5
C. 9
D. 10
Câu 10: Tổng các nghiệm nguyên của bất phương trình x (2-x) ≥ x (7-x) - 6 (x-1) trên đoạn (-10;10) bằng:
A. 5
B. 6
C. 21
D. 40
Câu 11: Bất phương trình (m-1) x>3 vô nghiệm khi
A. m≠1
B. m<1
C. m=1
D. m>1
Câu 12. Trên đường thẳng d1 cho 5 điểm phân biệt, trên đường thẳng d2 song song với đường thẳng d1, cho n điểm phân biệt. Biết có tất cả 175 tam giác được tạo thành mà 3 đỉnh lấy từ n + 5 điểm trên. Giá trị của n là
A. 10
B. 7
C. 8
D. 9
Câu 13: Cho bất phương trình bậc nhất hai ẩn x - 2y + 6 > 0
a) (0;0) có phải là một nghiệm của bất phương trình đã cho không?
b) Chỉ ra ba cặp số (x;y) là nghiệm của bất phương trình đã cho.
Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:












 Toán 10 Kết nối tri thức
Toán 10 Kết nối tri thức
 Toán 10 Chân trời sáng tạo
Toán 10 Chân trời sáng tạo
 Toán 10 Cánh Diều
Toán 10 Cánh Diều
 Soạn văn 10 Chân trời sáng tạo
Soạn văn 10 Chân trời sáng tạo
 Soạn văn 10 Cánh Diều
Soạn văn 10 Cánh Diều
 Soạn văn 10 Kết nối tri thức
Soạn văn 10 Kết nối tri thức
 Tiếng Anh 10 Global Success
Tiếng Anh 10 Global Success
 Tiếng anh 10 Friends Global
Tiếng anh 10 Friends Global
 Tiếng Anh 10 Explore New Worlds
Tiếng Anh 10 Explore New Worlds