Phương pháp giải phương trình vô tỷ chứa căn Cách giải phương trình vô tỉ chức căn

Tải về Bình luận

Cách giải phương trình vô tỷ chứa căn là tài liệu vô cùng hữu ích mà Eballsviet.com muốn giới thiệu đến quý thầy cô cùng các bạn học sinh tham khảo.

Phương pháp giải phương trình vô tỷ chứa căn gồm 44 trang tổng hợp các cách giải phương trình chứa căn kèm theo ví dụ minh họa và bài tập tự luyện. Hi vọng qua tài liệu này giúp các bạn lớp 12 học tập chủ động, nâng cao kiến thức để đạt kết quả cao trong kì thi THPT Quốc gia sắp tới. Bên cạnh đó các bạn xem thêm: 572 câu trắc nghiệm chuyên đề Hàm số nâng cao, 12 dạng toán về hàm ẩn liên quan đến sự tương giao của đồ thị hàm số.

Cách giải phương trình vô tỷ chứa căn

I. Các dạng bài tập bất phương trình chứa căn thức

1. Dạng bất phương trình chứa 1 căn bậc hai.

2. Dạng bất phương trình chứa 2 căn bậc hai.

3. Dạng bất phương trình chứa 2 căn có bậc khác nhau.

4. Dạng bất phương trình chứa nhiều căn.

II. Bất phương trình chứa 1 căn bậc hai.

Ví dụ 1: : Giải bất phương trình:

$\left(x^2-3 x\right) \sqrt{2 x^2-3 x-2} \geq 0, x \in \mathbb{R}$ $\left(x^2-3 x\right) \sqrt{2 x^2-3 x-2} \geq 0, x \in \mathbb{R}$

Đơn giản dạng $\mathrm{AB} \geq 0$ $\mathrm{AB} \geq 0$ nhưng rất nhiều học sinh không tìm ra được đầy đủ chức nghiệm của nó. Chúng ta cần sù̀ dưng phép biển đồi tương đương sau:

Gợi ý giải

Bất phương trình tương đương với:

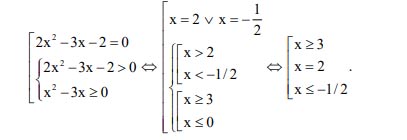
Vậy, tập nghiệm của bất phương trình là $\left(-\infty,-\frac{1}{2}\right] \cup\{2\} \cup[3 ;+\infty).$ $\left(-\infty,-\frac{1}{2}\right] \cup\{2\} \cup[3 ;+\infty).$

Luyện tập 1: Giải bất phương trình:

Nội dung chi tiết trọn bộ tài liệu:

Chia sẻ bởi:

Trịnh Thị Lương

Tải về

Liên kết tải về

Phương pháp giải phương trình vô tỷ chứa căn 474,2 KB Tải về

Chọn file cần tải:

Phương pháp giải phương trình vô tỷ chứa căn (.DOC) 1,9 MB Tải về

Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!