Đường trung tuyến: Tính chất, công thức tính đường trung tuyến Ôn tập Toán 7
Đường trung tuyến là gì? Cách tính đường trung tuyến như thế nào? Mời quý thầy cô cùng các bạn học sinh lớp 7 theo dõi bài viết dưới đây.

Đường trung tuyến là tài liệu hữu ích được biên soạn đầy đủ lý thuyết về khái niệm, công thức tính và các tính chất đường trung tuyến. Qua đó giúp học sinh củng cố, nắm vững chắc kiến thức nền tảng, vận dụng với các bài tập cơ bản để đạt được điểm số cao trong kì thi học kì môn Toán 7. Vậy sau đây là nội dung chi tiết tài liệu đường trung tuyến mời các bạn cùng theo dõi tại đây. Bên cạnh đó các bạn xem thêm tổng hợp kiến thức môn Toán lớp 7.
Đường trung tuyến
1. Đường trung tuyến là gì?
- Đường trung tuyến của đoạn thẳng là một đường thẳng đi qua trung điểm của đoạn thẳng đó.
- Đường trung tuyến trong tam giác là một đoạn thẳng nối từ đỉnh của tam giác tới trung điểm của cạnh đối diện. Mỗi tam giác sẽ có 3 đường trung tuyến.
2. Tính chất của đường trung tuyến trong tam giác
- Ba đường trung tuyến của tam giác cùng đi qua một điểm. Điểm đó cách đỉnh một khoảng bằng 2/3 độ dài đường trung tuyến đi qua đỉnh ấy.
- Giao điểm của ba đường trung tuyến gọi là trọng tâm.
- Vị trí của trọng tâm tam giác: Trọng tâm của một tam giác cách mỗi đỉnh một khoảng bằng 2/3 độ dài đường trung tuyến đi qua đỉnh ấy.
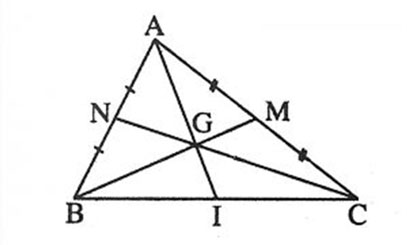
Gọi G là trọng tâm của tam giác ABC, ABC có các trung tuyến AI, BM, CN thì ta sẽ có biểu thức:
![]() \(\frac{AG}{AI}=\frac{BG}{BM}=\frac{CG}{CN}=\frac{2}{3}\)
\(\frac{AG}{AI}=\frac{BG}{BM}=\frac{CG}{CN}=\frac{2}{3}\)
a. Đường trung tuyến trong tam giác vuông
- Trong tam giác vuông, trung tuyến ứng với cạnh huyền bằng 1/2 cạnh huyền.
- Một tam giác có trung tuyến ứng với một cạnh bằng nửa cạnh đó thì tam giác ấy là tam giác vuông.
- Đường trung tuyến của tam giác vuông có đầy đủ các tính chất của một đường trung tuyến tam giác.
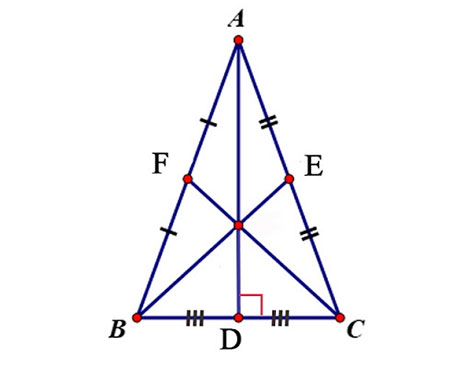
ABC vuông có AD là trung tuyến ứng với cạnh huyền BC.
=> AD = 1/2BC = DB = DC
Ngược lại, nếu trung tuyến AM = 1/2BC thì ABC vuông tại A.
b. Đường trung tuyến trong tam giác cân
- Đường trung tuyến ứng với cạnh đáy thì vuông góc với cạnh đáy. Và chia tam giác thành 2 tam giác bằng nhau.

ABC cân tại A có đường trung tuyến AD ứng với cạnh BC=> AD ⊥ BC và ΔADB = ΔADC
c. Đường trung tuyến trong tam giác đều
- 3 đường trung tuyến của tam giác đều sẽ chia tam giác đó thành 6 tam giác có diện tích bằng nhau.
- Trong tam giác đều đường thẳng đi qua một đỉnh bất kỳ và đi qua trọng tâm của tam giác sẽ chia tam giác đó thành 2 tam giác có diện tích bằng nhau.
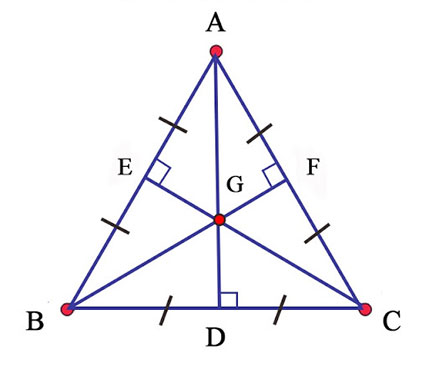
ΔABC đều => ΔGAE = ΔGAF = ΔGCF = ΔGCD = ΔGBD = ΔGBE = ΔGEB = ΔGEA
SADB = SADC = SCEA = SCEB = SBFA = SBFC
3. Công thức tính đường trung tuyến của tam giác
Độ dài đường trung tuyến của một tam giác được tính thông qua độ dài các cạnh của tam giác và được tính bằng định lý Apollonnius.
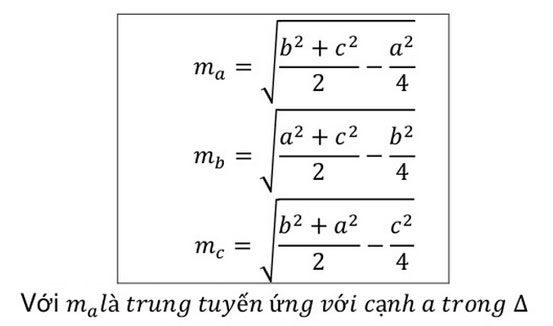
Trong đó:
- a, b, c: là các cạnh của tam giác.
- ma, mb, mc: là các đường trung tuyến của tam giác.
Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:












 Lớp 2
Lớp 2
 Lớp 4
Lớp 4
 Lớp 5
Lớp 5
 Thi vào 6
Thi vào 6
 Lớp 6
Lớp 6
 Lớp 7
Lớp 7
 Lớp 9
Lớp 9









