Đề thi thử Đại học năm 2013 - môn Toán (Đề 26) Đề thi thử số 26
ĐỀ THI THỬ ĐẠI HỌC - CAO ĐẲNG
NĂM 2012 - 2013
MÔN THI: TOÁN
Đề số 26
PHẦN CHUNG CHO TẤT CẢ CÁC THÍ SINH (7 điểm)
Câu I (2 điểm) Cho hàm số y = f(x) = 8x4 - 9x2 + 1
1. Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số.
2. Dựa vào đồ thị (C) hãy biện luận theo m số nghiệm của phương trình:
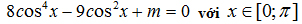
Câu II (2 điểm): Giải phương trình, hệ phương trình:
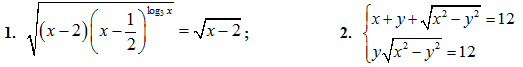
Câu III: Tính diện tích của miền phẳng giới hạn bởi các đường y = |x2 - 4x| và y = 2x
Câu IV (1 điểm) Cho hình chóp cụt tam giác đều ngoại tiếp một hình cầu bán kính r cho trước. Tính thể tích hình chóp cụt biết rằng cạnh đáy lớn gấp đôi cạnh đáy nhỏ.
Câu V (1 điểm) Định m để phương trình sau có nghiệm:
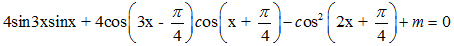
PHẦN RIÊNG (3 điểm): Thí sinh chỉ làm một trong hai phần (Phần 1 hoặc phần 2)
1. Theo chương trình chuẩn.
Câu VI.a (2 điểm)
1. Cho ABC có đỉnh A(1;2), đường trung tuyến BM: 2x + y + 1 = 0 và phân giác trong CD: x + y - 1 = 0. Viết phương trình đường thẳng BC.
2. Cho đường thẳng (D) có phương trình: 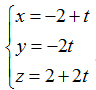
Gọi ∆ là đường thẳng qua điểm A(4;0;-1) song song với (D) và I(-2;0;2) là hình chiếu vuông góc của A trên (D). Trong các mặt phẳng qua ∆, hãy viết phương trình của mặt phẳng có khoảng cách đến (D) là lớn nhất.
Câu VII.a (1 điểm) Cho x, y, z là 3 số thực thuộc (0;1]. Chứng minh rằng:
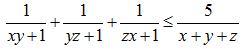
2. Theo chương trình nâng cao.
Câu VI.b (2 điểm)
1. Cho hình bình hành ABCD có diện tích bằng 4. Biết A(1;0), B(0;2) và giao điểm I của hai đường chéo nằm trên đường thẳng y = x. Tìm tọa độ đỉnh C và D.
2. Cho hai điểm A(1;5;0), B(3;3;6) và đường thẳng ∆ có phương trình tham số 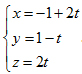 . Một điểm M thay đổi trên đường thẳng ∆ , tìm điểm M để chu vi tam giác MAB đạt giá trị nhỏ nhất.
. Một điểm M thay đổi trên đường thẳng ∆ , tìm điểm M để chu vi tam giác MAB đạt giá trị nhỏ nhất.
Câu VII.b (1 điểm) Cho a, b, c là ba cạnh tam giác. Chứng minh:
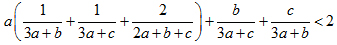
Download tài liệu để xem thêm chi tiết
Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:












 Lớp 2
Lớp 2
 Lớp 4
Lớp 4
 Lớp 5
Lớp 5
 Thi vào 6
Thi vào 6
 Lớp 6
Lớp 6
 Lớp 7
Lớp 7
 Lớp 9
Lớp 9









