Đề thi học sinh giỏi Toán thành phố Hà Nội năm 2013 - 2014

Tải về Bình luận

ĐỀ THI HỌC SINH GIỎI TOÁN THÀNH PHỐ HÀ NỘI
Năm học: 2013 - 2014

Thời gian làm bài: 180 phút

Bài 1: (5 điểm)

Cho hàm số y = x³ -3x + 4 có đồ thị (C)

a. Tìm các điểm M, N cùng nằm trên (C) sao cho điểm I(-1/2; 2) là trung điểm của đoạn thẳng MN.

b. Cho ba điểm phân biệt A, B, C cùng thuộc (C). Các tiếp tuyến của (C) tại A, B, C cắt (C) tại điểm thứ hai lần lượt là A'; B'; C'. Chứng minh rằng nếu A, B, C thẳng hàng thì A’, B’, C’ cũng thẳng hàng.

Bài 2: (5 điểm)

a. Giải phương trình:

b. Giải hệ phương trình: 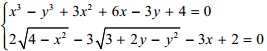Đề thi học sinh giỏi Toán thành phố Hà Nội năm 2013 - 2014

Bài 3: (2 điểm)

Cho các số thực a, b, c sao cho a ≥ 0, b ≥ 0, 0 ≤ c ≤ 1 và a² + b² + c² = 3. Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức sau:

Bài 4: (3 điểm)

Trong không gian cho ba tia Ox, Oy, Oz không đồng phẳng. Đặt góc xOy = α, góc yOz = β, góc zOx = γ. Lấy các điểm A, B, C lần lượt trên các tia Ox, Oy, Oz sao cho OA = OB = OC = a với a > 0.

a. Gọi M là điểm nằm trên đoạn BC sao cho BM = 2MC và I là trung điểm của đoạn thẳng AM. Tính độ dài đoạn thẳng OI theo α trong trường hợp α = γ = 60^o, β = 90^o

b. Chứng minh rằng: cosα + cosγ + cosβ > -3/2

Bài 5: (3 điểm)

Cho dãy số (u_n) thỏa mãn điều kiện: 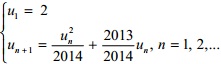Đề thi học sinh giỏi Toán thành phố Hà Nội năm 2013 - 2014

a. Chứng minh rằng (u_n) là dãy số tăng

b. Với mỗi n ≥ 1, n thuộc N, đặt . Chứng minh rằng: v₁ + v₂ + ... + v_n < 2014 với mọi n ≥ 1.

Download tài liệu để xem chi tiết.

Chia sẻ bởi:

Nguyễn Thu Ngân

Tải về

Liên kết tải về

Đề thi học sinh giỏi Toán thành phố Hà Nội năm 2013 - 2014 157 KB Tải về

Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!