Công thức con lắc lò xo Công thức Vật lý 12
Công thức con lắc lò xo là tài liệu vô cùng hữu ích tổng hợp kiến thức về khái niệm, cấu tạo của con lắc lò xo, công thức tính ví dụ minh họa kèm theo các dạng bài tập trọng tâm. Thông qua tài liệu này các bạn có thêm nhiều tài liệu học tập nhanh chóng ghi nhớ kiến thức để biết cách giải các bài tập Vật lí.
Công thức con lắc lò xo được vận dụng nhiều trong trình Vật lí lớp 12. Con lắc lò xo chính là một hệ gồm một vật nặng kích thước nhỏ có khối lượng m gắn vào một đầu của lò xo, có độ cứng k, đầu còn lại của lò xo được gắn hoặc treo vào một điểm cố định. Vậy sau đây là toàn bộ kiến thức về con lắc lò xo mời các bạn theo dõi. Ngoài ra các bạn xem thêm công thức Vật lí 12.
Tổng hợp công thức con lắc lò xo
1. Con lắc lò xo là gì
Con lắc lò xo là một hệ gồm một vật nặng kích thước nhỏ có khối lượng m gắn vào một đầu của lò xo, có độ cứng k, đầu còn lại của lò xo được gắn hoặc treo vào một điểm cố định. Có thể bố trí cho con lắc lò xo dao động theo phương ngang, theo phương thẳng đứng hoặc theo phương của một dốc nghiêng.
Dựa theo định nghĩa trên ta có 3 loại con lắc lò xo:
- Con lắc nằm ngang: Dạng này cần học kĩ.
- Con lắc phương thẳng đứng: Trong quá trình học ta chỉ khảo sát con lắc treo theo phương thẳng đứng bởi dạng này thường xuyên ra vào đề thi của BGD&ĐT.
- Con lắc nằm nghiêng: Phần này ta có thể lược bỏ vì nhiều năm trở lại đề thi không ra.
- Phương trình ly độ của con lắc:
![]() \(x = A\cos \left( {\omega t + \varphi } \right)\)
\(x = A\cos \left( {\omega t + \varphi } \right)\)
- Cấu tạo của con lắc lò xo
Con lắc lò xo gồm một vật nhỏ có khối lượng m gắn vào đầu của một lò xo có độ cứng k, có khối lượng không đáng kể. Đầu kia của lò xo được giữ cố định. Vật m có thể trượt trên một mặt phẳng nằm ngang không có ma sát.
Vị trí cân bằng của vật là vị trí khi lò xo không biến dạng. Vật sẽ đứng yên mãi ở vị trí này nếu lúc đầu nó đứng yên.
Kéo vật ra khỏi vị trí cân bằng cho lò xo dãn ra một đoạn nhỏ rồi buông tay, ta thấy vật dao động trên một đoạn thẳng quanh vị trí cân bằng.
2. Chu kì và tần số của con lắc lò xo
- Tần số góc của con lắc lò xo: ![]() \(\omega = \frac{k}{m} = \sqrt {\frac{g}{{\Delta {l_0}}}}\)
\(\omega = \frac{k}{m} = \sqrt {\frac{g}{{\Delta {l_0}}}}\)
- Công thức chu kì của con lắc lò xo:  \(T = \frac{{2\pi }}{\omega } = 2\pi \sqrt {\frac{m}{k}} = 2\pi \sqrt {\frac{{\Delta {l_0}}}{k}}\)
\(T = \frac{{2\pi }}{\omega } = 2\pi \sqrt {\frac{m}{k}} = 2\pi \sqrt {\frac{{\Delta {l_0}}}{k}}\)
- Tần số của con lắc lò xo: ![]() \(f = \frac{1}{T} = \frac{1}{{2\pi }}\sqrt {\frac{k}{m}}\)
\(f = \frac{1}{T} = \frac{1}{{2\pi }}\sqrt {\frac{k}{m}}\)
Chú ý: Nếu trong thời gian vật thực hiện được N dao động thì tần số là: ![]() \(f = \frac{N}{t}\)
\(f = \frac{N}{t}\)
| Khối lượng vật | ||
| Chu kì | ||
| Tần số |
- Thời gian nén và giãn của lò xo:  \(\left\{ {\begin{array}{*{20}{c}} {{t_{nen}} = \dfrac{{{\varphi _{nen}}}}{\omega }} \\ {{t_{nen}} + {t_{dan}} = T} \end{array}} \right.\). Trong đó:
\(\left\{ {\begin{array}{*{20}{c}} {{t_{nen}} = \dfrac{{{\varphi _{nen}}}}{\omega }} \\ {{t_{nen}} + {t_{dan}} = T} \end{array}} \right.\). Trong đó:  \(\left\{ {\begin{array}{*{20}{c}}
{{\varphi _{nen}} = 2\alpha } \\
{\cos \alpha = \dfrac{{\Delta l}}{{Aa}}}
\end{array}} \right.\)
\(\left\{ {\begin{array}{*{20}{c}}
{{\varphi _{nen}} = 2\alpha } \\
{\cos \alpha = \dfrac{{\Delta l}}{{Aa}}}
\end{array}} \right.\)
| Ghép nối tiếp | Ghép song song | |
| Hình vẽ minh họa | 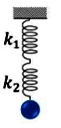 |
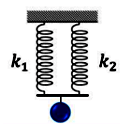 |
| Độ cứng của lò xo | ||
| Chu kỳ |
3. Năng lượng của con lắc lò xo
a. Động năng của con lắc lò xo (J)
![]() \({W_d} = \frac{1}{2}m{v^2} = \frac{1}{2}m{\omega ^2}{A^2}{\sin ^2}\left( {\omega t + \varphi } \right)\)
\({W_d} = \frac{1}{2}m{v^2} = \frac{1}{2}m{\omega ^2}{A^2}{\sin ^2}\left( {\omega t + \varphi } \right)\)
- Động năng cực đại: ![]() \({W_{d\max }} = \frac{1}{2}m{v^2}_{\max }\) với vmax là vận tốc cực đại. đv: m/s
\({W_{d\max }} = \frac{1}{2}m{v^2}_{\max }\) với vmax là vận tốc cực đại. đv: m/s
b. Thế năng của con lắc lò xo (J)
![]() \({W_t} = \frac{1}{2}k{x^2} = \frac{1}{2}m{\omega ^2}{A^2}{\cos ^2}\left( {\omega t + \varphi } \right)\)
\({W_t} = \frac{1}{2}k{x^2} = \frac{1}{2}m{\omega ^2}{A^2}{\cos ^2}\left( {\omega t + \varphi } \right)\)
- Thế năng cực đại: ![]() \({W_{t\max }} = \frac{1}{2}k{x^2}_{\max } = \frac{1}{2}k{A^2}\)
\({W_{t\max }} = \frac{1}{2}k{x^2}_{\max } = \frac{1}{2}k{A^2}\)
c. Cơ năng của con lắc lò xo (năng lượng toàn phần) (J)
![]() \(W = {W_d} + {W_t} = \frac{1}{2}k{A^2} = \frac{1}{2}m{\omega ^2}{A^2}\)
\(W = {W_d} + {W_t} = \frac{1}{2}k{A^2} = \frac{1}{2}m{\omega ^2}{A^2}\)
- Cơ năng của con lắc tỉ lệ với bình phương biên độ dao động, không phụ thuộc vào khối lượng vật nặng.
- Nếu tại t1 ta có x1, v1 và tại t2 ta có x2, v2. Tìm ω, A thì ta có công thức:  \(\left\{ {\begin{array}{*{20}{c}}
{\omega = \sqrt {\dfrac{{{v_2}^2 - {v_1}^2}}{{{x_1}^2 - {x_2}^2}}} } \\
{A = \sqrt {{x_1}^2 + \dfrac{{{v_1}^2}}{{{\omega ^2}}}} }
\end{array}} \right.\)
\(\left\{ {\begin{array}{*{20}{c}}
{\omega = \sqrt {\dfrac{{{v_2}^2 - {v_1}^2}}{{{x_1}^2 - {x_2}^2}}} } \\
{A = \sqrt {{x_1}^2 + \dfrac{{{v_1}^2}}{{{\omega ^2}}}} }
\end{array}} \right.\)
- Cho biết k; m và W. Tìm vmax và amax:  \(\left\{ {\begin{array}{*{20}{c}}
{{v_{\max }} = \omega .A} \\
{{a_{\max }} = {v_{\max }}.\omega = \dfrac{{{v^2}_{\max }}}{A}}
\end{array}} \right.\)
\(\left\{ {\begin{array}{*{20}{c}}
{{v_{\max }} = \omega .A} \\
{{a_{\max }} = {v_{\max }}.\omega = \dfrac{{{v^2}_{\max }}}{A}}
\end{array}} \right.\)
- Khi  \({W_d} = n{W_t} \Rightarrow \left\{ {\begin{array}{*{20}{c}}
{x = \pm \dfrac{A}{{\sqrt {n + 1} }}} \\
\begin{gathered}
a = \pm \dfrac{{{a_{\max }}}}{{\sqrt {n + 1} }} \hfill \\
v = \pm \dfrac{{{v_{\max }}}}{{\sqrt {\frac{1}{n} + 1} }} \hfill \\
\end{gathered}
\end{array}} \right.\)
\({W_d} = n{W_t} \Rightarrow \left\{ {\begin{array}{*{20}{c}}
{x = \pm \dfrac{A}{{\sqrt {n + 1} }}} \\
\begin{gathered}
a = \pm \dfrac{{{a_{\max }}}}{{\sqrt {n + 1} }} \hfill \\
v = \pm \dfrac{{{v_{\max }}}}{{\sqrt {\frac{1}{n} + 1} }} \hfill \\
\end{gathered}
\end{array}} \right.\)
- Khoảng thời gian ngắn nhất giữa hai lần liên tiếp động năng bằng thế năng là: ![]() \(\frac{T}{4}\)
\(\frac{T}{4}\)
- Khoảng thời gian 2 lần liên tiếp động năng hoặc thế năng bằng không là: ![]() \(\frac{T}{2}\)
\(\frac{T}{2}\)
4. Công thức con lắc lò xo nằm ngang
- Với con lắc lò xo nằm ngang thì lực kéo về và lực đàn hồi là một (vì tại VTCB lò xo không biến dạng)
- Lực đàn hồi: Fđh = k.x (x: là li độ)
+ Lực đàn hồi cực đại: Fđhmax = k.A (A: biên độ dao động)
+ Lực đàn hồi cực tiểu : Fmin = 0
5. Công thức con lắc lò xo thẳng đứng
- Chiều dài lò xo tại VTCB: lcb = l0 + Δl
+ Chiều dài cực tiểu (khi vật ở vị trí cao nhất): lmin = l0 + Δl – A
+ Chiều dài cực đại (khi vật ở vị trí thấp nhất): lmax = l0 + Δl + A
- Với con lắc lò xo thẳng đứng hoặc đặt trên mặt phẳng nghiêng thì độ lớn lực đàn hồi có biểu thức:
* Fđh = k|Δl + x| với chiều dương hướng xuống
* Fđh = k|Δl – x| với chiều dương hướng lên
a. Nếu Δl >A:
- Lực đàn hồi cực đại : Fmax = k(Δl + A)
- Lực đàn hồi cực tiểu : Fmin = k(Δl – A)
b. Nếu Δl < A:
- Lực đàn hồi cực đại : Fmax = k(A – Δl) ; lúc vật ở vị trí cao nhất
- Lực đàn hồi cực tiểu: Fmin = 0 (lúc vật đi qua vị trí lò xo không biến dạng)
c. Khi ở vị trí cân bằng thì: Fđh = k.Δl = mg
6. Bài tập về con lắc lò xo
Câu 1: Một con lắc lò xo có biên độ 5cm, tốc độ cực đại 50cm/s và có cơ năng là 0,5J. Tính:
a. Độ cứng của lò xo.
b. Khối lượng vật nặng.
c. Động năng của vật nặng tại vị trí x = 2cm.
Hướng dẫn giải
a. Ta có: ![]() \(\left\{ {\begin{array}{*{20}{c}}
{A = 5cm} \\
{{v_{\max }} = 50cm/s}
\end{array}} \right.\)
\(\left\{ {\begin{array}{*{20}{c}}
{A = 5cm} \\
{{v_{\max }} = 50cm/s}
\end{array}} \right.\)
 \(\begin{gathered}
\Rightarrow {v_{\max }} = A.\omega \Leftrightarrow \frac{5}{{100}} = 5.\omega \Rightarrow \omega = 10\left( {rad/s} \right) \hfill \\
W = 5J \Rightarrow k = \frac{{2W}}{{{A^2}}} = \frac{{2.0,5}}{{{{\left( {0,05} \right)}^2}}} = 400\left( {N/m} \right) \hfill \\
\end{gathered}\)
\(\begin{gathered}
\Rightarrow {v_{\max }} = A.\omega \Leftrightarrow \frac{5}{{100}} = 5.\omega \Rightarrow \omega = 10\left( {rad/s} \right) \hfill \\
W = 5J \Rightarrow k = \frac{{2W}}{{{A^2}}} = \frac{{2.0,5}}{{{{\left( {0,05} \right)}^2}}} = 400\left( {N/m} \right) \hfill \\
\end{gathered}\)
b. Ta có: ![]() \(m = \frac{k}{{{\omega ^2}}} = \frac{{400}}{{{{10}^2}}} = 4\left( {kg} \right)\)
\(m = \frac{k}{{{\omega ^2}}} = \frac{{400}}{{{{10}^2}}} = 4\left( {kg} \right)\)
c. Ta có: x = 2cm
 \(\begin{gathered}
\Rightarrow {W_t} = \frac{1}{2}k.{x^2} = \frac{1}{2}.400.{\left( {0,02} \right)^2} = 0,08\left( J \right) \hfill \\
\Rightarrow {W_d} = W - {W_t} = 0,5 - 0,08 = 0,42\left( J \right) \hfill \\
\end{gathered}\)
\(\begin{gathered}
\Rightarrow {W_t} = \frac{1}{2}k.{x^2} = \frac{1}{2}.400.{\left( {0,02} \right)^2} = 0,08\left( J \right) \hfill \\
\Rightarrow {W_d} = W - {W_t} = 0,5 - 0,08 = 0,42\left( J \right) \hfill \\
\end{gathered}\)
Câu 2: Một con lắc lò xo có độ cứng k treo vật có khối lượng m1 dao động chu kì T1 = 0,6s, treo m2 chu kì T2 = 0,8s. Hỏi treo m1, m2 với chu kì bao nhiêu?
Hướng dẫn giải
 \(\begin{matrix}
{T_1} = 2\pi \sqrt {\dfrac{{{m_1}}}{k}} \Rightarrow {T_1} = 4{\pi ^2}\left( {\dfrac{{{m_1}}}{k}} \right) \hfill \\
{T_2} = 2\pi \sqrt {\dfrac{{{m_2}}}{k}} \Rightarrow {T_1} = 4{\pi ^2}\left( {\dfrac{{{m_2}}}{k}} \right) \hfill \\
T = 2\pi \sqrt {\dfrac{{{m_1} + {m_2}}}{k}} \hfill \\
\Rightarrow {T^2} = 4{\pi ^2}\left( {\dfrac{{{m_1} + {m_2}}}{k}} \right) \hfill \\
\Rightarrow {T^2} = 4{\pi ^2}\dfrac{{{m_1}}}{k} + 4{\pi ^2}\dfrac{{{m_2}}}{k} = {T_1}^2 + {T_2}^2 \hfill \\
\Rightarrow {T^2} = 0,{6^2} + 0,{8^2} = 1\left( s \right) \hfill \\
\end{matrix}\)
\(\begin{matrix}
{T_1} = 2\pi \sqrt {\dfrac{{{m_1}}}{k}} \Rightarrow {T_1} = 4{\pi ^2}\left( {\dfrac{{{m_1}}}{k}} \right) \hfill \\
{T_2} = 2\pi \sqrt {\dfrac{{{m_2}}}{k}} \Rightarrow {T_1} = 4{\pi ^2}\left( {\dfrac{{{m_2}}}{k}} \right) \hfill \\
T = 2\pi \sqrt {\dfrac{{{m_1} + {m_2}}}{k}} \hfill \\
\Rightarrow {T^2} = 4{\pi ^2}\left( {\dfrac{{{m_1} + {m_2}}}{k}} \right) \hfill \\
\Rightarrow {T^2} = 4{\pi ^2}\dfrac{{{m_1}}}{k} + 4{\pi ^2}\dfrac{{{m_2}}}{k} = {T_1}^2 + {T_2}^2 \hfill \\
\Rightarrow {T^2} = 0,{6^2} + 0,{8^2} = 1\left( s \right) \hfill \\
\end{matrix}\)
Câu 3: Một con lắc lò xo gồm vật nặng có khối lượng m = 0,2 kg và lò xo có độ cứng k = 20N/m đang dao động điều hòa với biên độ 6cm. Tính vận tốc của vật khi đi qua vị trí có thế năng bằng 3 động năng.
Hướng dẫn giải
Ta có: ![]() \({W_t} = 3.{W_d}\)
\({W_t} = 3.{W_d}\)
 \(\begin{matrix}
\Rightarrow {W_d} = \dfrac{1}{3}.{W_t} \hfill \\
\Rightarrow \left| x \right| = \dfrac{A}{{\sqrt {n + 1} }} = \dfrac{A}{{\sqrt {\dfrac{1}{3} + 1} }} = \dfrac{{A\sqrt 3 }}{2} \hfill \\
\Rightarrow \left| v \right| = \dfrac{{{v_{\max }}}}{2} = \dfrac{{\omega .A}}{2} \hfill \\
\end{matrix}\)
\(\begin{matrix}
\Rightarrow {W_d} = \dfrac{1}{3}.{W_t} \hfill \\
\Rightarrow \left| x \right| = \dfrac{A}{{\sqrt {n + 1} }} = \dfrac{A}{{\sqrt {\dfrac{1}{3} + 1} }} = \dfrac{{A\sqrt 3 }}{2} \hfill \\
\Rightarrow \left| v \right| = \dfrac{{{v_{\max }}}}{2} = \dfrac{{\omega .A}}{2} \hfill \\
\end{matrix}\)
Mà  \(\omega = \sqrt {\frac{k}{m}} = \sqrt {\frac{{20}}{{0,2}}} = 10\left( {rad/s} \right)\)
\(\omega = \sqrt {\frac{k}{m}} = \sqrt {\frac{{20}}{{0,2}}} = 10\left( {rad/s} \right)\)
![]() \(\Rightarrow \left| v \right| = \frac{{10.0,06}}{2} = 0,3\left( {m/s} \right)\)
\(\Rightarrow \left| v \right| = \frac{{10.0,06}}{2} = 0,3\left( {m/s} \right)\)
Vậy khi đi qua vị trí có thế năng bằng 3 động năng vận tốc của vật là 0,3m/s.
Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:












 Đề thi học kì 1 Lớp 12
Đề thi học kì 1 Lớp 12
 Đề thi giữa học kì 1 Lớp 12
Đề thi giữa học kì 1 Lớp 12
 Đề thi giữa học kì 2 Lớp 12
Đề thi giữa học kì 2 Lớp 12
 Đề thi học kì 2 Lớp 12
Đề thi học kì 2 Lớp 12
 Soạn Văn 12 KNTT
Soạn Văn 12 KNTT
 Soạn Văn 12 CTST
Soạn Văn 12 CTST
 Soạn Văn 12 Cánh Diều
Soạn Văn 12 Cánh Diều
 Văn 12
Văn 12
 Toán 12 Chân trời sáng tạo
Toán 12 Chân trời sáng tạo









