Các phương pháp tính thể tích khối đa diện Tài liệu ôn tập môn Toán lớp 12
Mời quý thầy cô giáo cùng các bạn học sinh lớp 12 cùng tham khảo tài liệu Các phương pháp tính thể tích khối đa diện được chúng tôi tổng hợp và đăng tải ngay sau đây.
Đây là tài liệu cực kì hữu ích, gồm 34 trang hướng dẫn các phương pháp tính thể tích khối đa diện và các bài tập vận dụng. Hy vọng với tài liệu này các bạn học sinh có thêm nhiều tài liệu tham khảo, củng cố nắm vững kiến thức thể tích khối đa diện để đạt được kết quả cao trong các bài kiểm tra, bài thi THPT Quốc gia sắp tới. Đồng thời đây cũng là tư liệu tham khảo dành cho các giáo viên giảng dạy. Nội dung chi tiết mời bạn đọc cùng tham khảo và tải tài liệu tại đây.
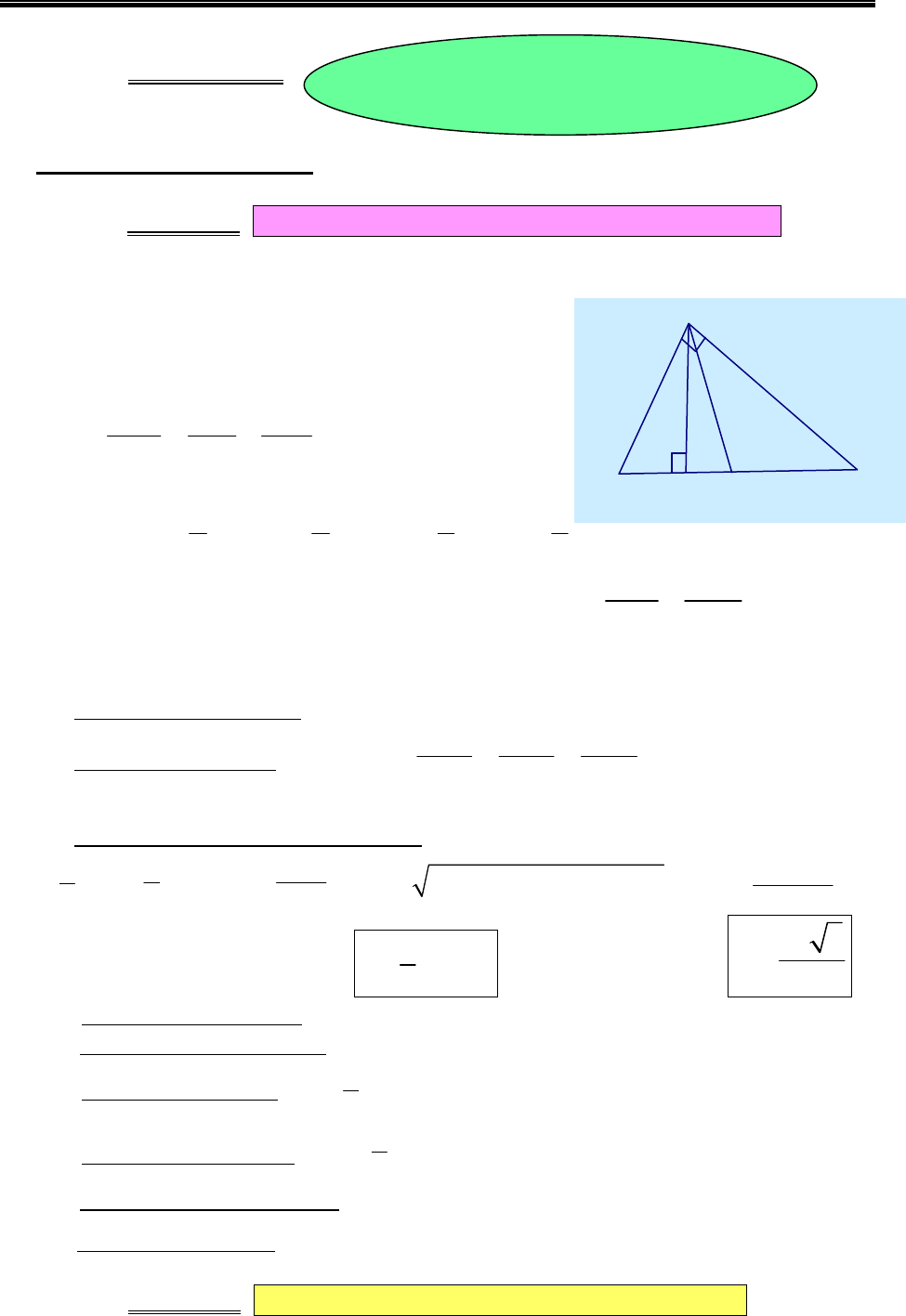
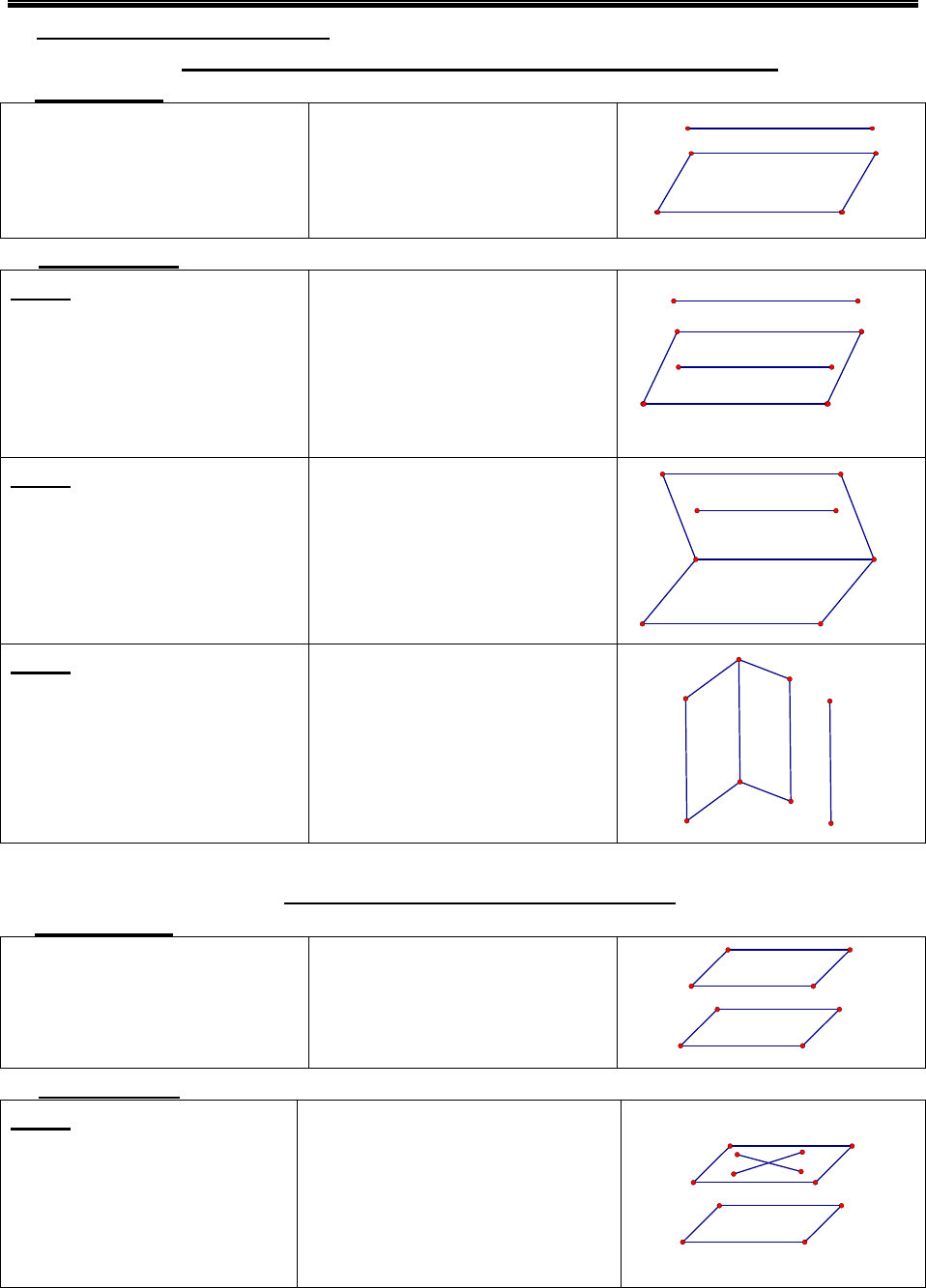
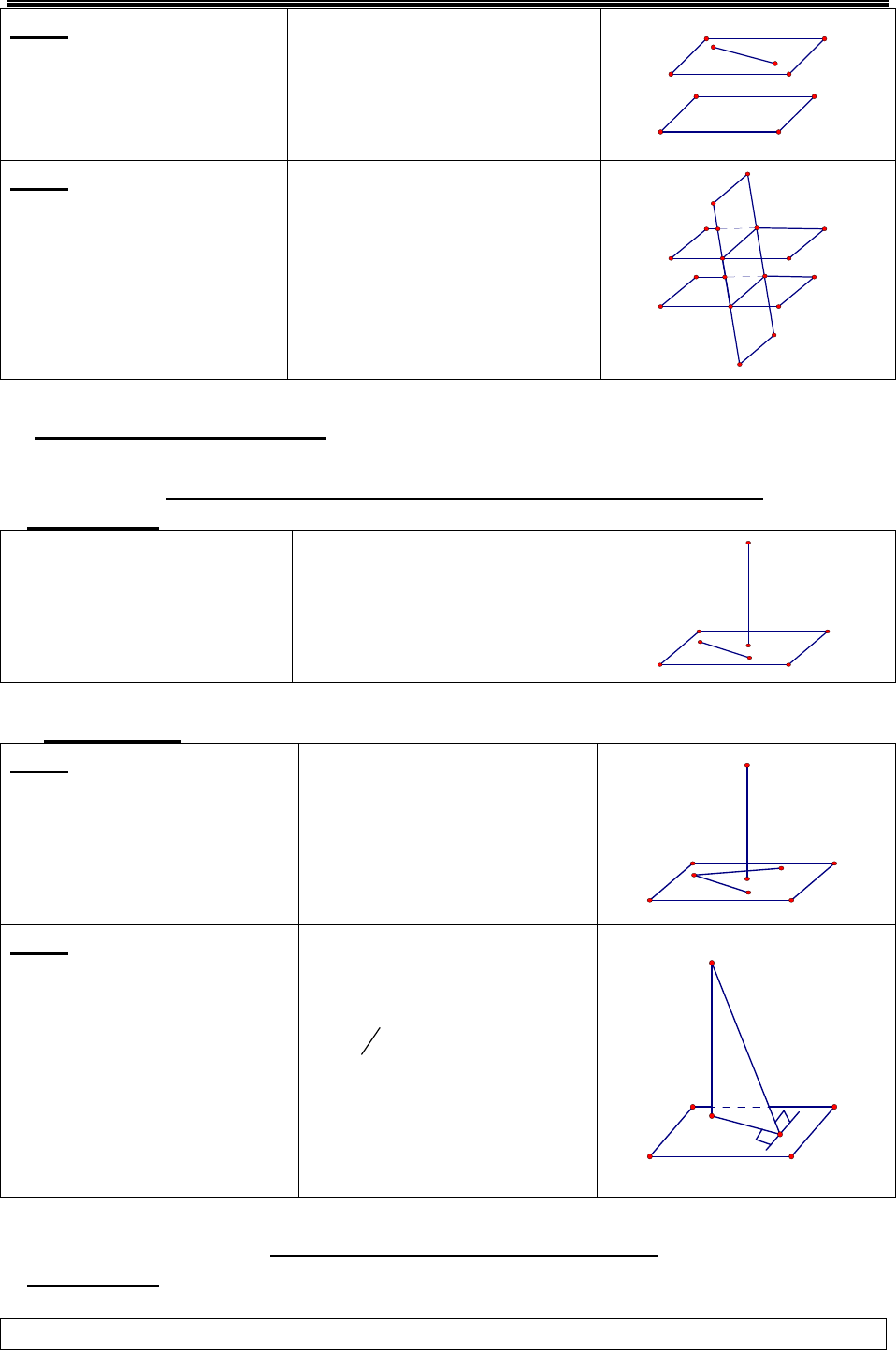
Các phương pháp tính thể tích khối đa diện
Thể tích khối đa diện – www.mathvn.com
http://book.mathvn.com
1
c
b
a
M
H
C
B
A
CHUYÊN ĐỀ: PHƯƠNG PHÁP LUYỆN TẬP
THỂ TÍCH KHỐI ĐA DIỆN
I. Ôn tập kiến thức cơ bản:
ÔN TẬP 1. KIẾN THỨC CƠ BẢN HÌNH HỌC LỚP 9 - 10
1. Hệ thức lượng trong tam giác vuông : cho
ABC
D
vuông ở A ta có :
a) Định lý Pitago :
2 2 2
BC AB AC
= +
b)
CBCHCABCBHBA .;.
22
==
c) AB. AC = BC. AH
d)
222
111
AC
AB
AH
+=
e) BC = 2AM
f)
sin , os , tan ,cot
b c b c
B c B B B
a a c b
= = = =
g) b = a. sinB = a.cosC, c = a. sinC = a.cosB, a =
sin cos
b b
B C
=
,
b = c. tanB = c.cot C
2.Hệ thức lượng trong tam giác thường:
* Định lý hàm số Côsin: a
2
= b
2
+ c
2
- 2bc.cosA
* Định lý hàm số Sin:
2
sin sin sin
a b c
R
A B C
= = =
3. Các công thức tính diện tích.
a/ Công thức tính diện tích tam giác:
1
2
S
=
a.h
a
=
1 . .
. sin . .( )( )( )
2 4
a b c
a b C p r p p a p b p c
R
= = = - - -
với
2
a b c
p
+ +
=
Đặc biệt :*
ABC
D
vuông ở A :
1
.
2
S AB AC
=
,*
ABC
D
đều cạnh a:
2
3
4
a
S =
b/ Diện tích hình vuông : S = cạnh x cạnh
c/ Diện tích hình chữ nhật : S = dài x rộng
d/ Diên tích hình thoi : S =
1
2
(chéo dài x chéo ngắn)
d/ Diện tích hình thang :
1
2
S
=
(đáy lớn + đáy nhỏ) x chiều cao
e/ Diện tích hình bình hành : S = đáy x chiều cao
f/ Diện tích hình tròn :
2
S .
R
p
=
ÔN TẬP 2 KIẾN THỨC CƠ BẢN HÌNH HỌC LỚP 11
Thể tích khối đa diện – www.mathvn.com
http://book.mathvn.com
2
A.QUAN HỆ SONG SONG
§1.ĐƯỜNG THẲNG VÀ MẶT PHẲNG SONG SONG
I. Định nghĩa:
Đường thẳng và mặt
phẳng gọi là song song
với nhau nếu chúng
không có điểm nào chung.
a//(P) a (P)
Û Ç =Æ
a
(P)
II.Các định lý:
ĐL1:Nếu đường thẳng d
không nằm trên mp(P) và
song song với đường
thẳng a nằm trên mp(P)
thì đường thẳng d song
song với mp(P)
d (P)
d/ /a d/ /(P)
a (P)
ì
Ë
ï
Þ
í
ï
Ì
î
d
a
(P)
ĐL2: Nếu đường thẳng a
song song với mp(P) thì
mọi mp(Q) chứa a mà cắt
mp(P) thì cắt theo giao
tuyến song song với a.
a/ /(P)
a (Q) d/ /a
(P) (Q) d
ì
ï
Ì Þ
í
ï
Ç =
î
d
a
(Q)
(P)
ĐL3: Nếu hai mặt phẳng
cắt nhau cùng song song
với một đường thẳng thì
giao tuyến của chúng
song song với đường
thẳng đó.
(P) (Q) d
(P)/ /a d/ /a
(Q)/ /a
ì
Ç =
ï
Þ
í
ï
î
a
d
Q
P
§2.HAI MẶT PHẲNG SONG SONG
I. Định nghĩa:
Hai mặt phẳng được gọi
là song song với nhau nếu
chúng không có điểm nào
chung.
(P)/ /(Q) (P) (Q)
Û Ç =Æ
Q
P
II.Các định lý:
ĐL1: Nếu mp(P) chứa
hai đường thẳng a, b cắt
nhau và cùng song song
với mặt phẳng (Q) th
ì
(P) và (Q) song song với
nhau.
a,b (P)
a b I (P)/ /(Q)
a/ /(Q),b/ /(Q)
ì
Ì
ï
Ç = Þ
í
ï
î
I
b
a
Q
P
Thể tích khối đa diện – www.mathvn.com
http://book.mathvn.com
3
ĐL2: Nếu một đường
thẳng nằm một trong hai
mặt phẳng song song thì
song song với mặt phẳng
kia.
(P)/ /(Q)
a / /(Q)
a (P)
ì
Þ
í
Ì
î
a
Q
P
ĐL3: Nếu hai mặt phẳng
(P) và (Q) song song thì
mọi mặt phẳng (R) đã
cắt (P) thì phải cắt (Q) và
các giao tuyến của chúng
song song.
(P) / /(Q)
(R) (P) a a / /b
(R) (Q) b
ì
ï
Ç = Þ
í
ï
Ç =
î
b
a
R
Q
P
B.QUAN HỆ VUÔNG GÓC
§1.ĐƯỜNG THẲNG VUÔNG GÓC VỚI MẶT PHẲNG
I.Định nghĩa:
Một đường thẳng được
gọi là vuông góc với một
mặt phẳng nếu nó vuông
góc với mọi đường thẳng
nằm trên mặt phẳng đó.
a mp(P) a c, c (P)
^ Û ^ " Ì
P
c
a
II. Các định lý:
ĐL1: Nếu đường thẳng d
vuông góc với hai đường
thẳng cắt nhau a và b
cùng nằm trong mp(P) thì
đường thẳng d vuông góc
với mp(P).
d a,d b
a,b mp(P) d mp(P)
a,b caét nhau
ì
^ ^
ï
Ì Þ ^
í
ï
î
d
a
b
P
ĐL2: (Ba đường vuông
góc) Cho đường thẳng a
không vuông góc với
mp(P) và đường thẳng b
nằm trong (P). Khi đó,
điều kiện cần và đủ để b
vuông góc với a là b
vuông góc với hình chiếu
a’ của a trên (P).
a mp(P),b mp(P)
b a b a'
^ Ì
^ Û ^
a'
a
b
P
§2.HAI MẶT PHẲNG VUÔNG GÓC
I.Định nghĩa:
Hai mặt phẳng được gọi là vuông góc với nhau nếu góc giữa chúng bằng 90
0
.
Chia sẻ bởi: 
Trịnh Thị Thanh
Trịnh Thị Thanh Liên kết tải về
Các phương pháp tính thể tích khối đa diện 443,4 KB Tải về
Có thể bạn quan tâm
-
Văn mẫu lớp 12: Dàn ý phân tích nhân vật người đàn bà hàng chài (11 Mẫu + Sơ đồ tư duy)
-
Phân tích tác phẩm Giàn bầu trước ngõ của Nguyễn Ngọc Tư
-
Văn mẫu lớp 12: Phân tích nhân vật Trương Ba trong Hồn Trương Ba da hàng thịt
-
Phân tích nhân vật bé Em trong truyện Áo Tết
-
Văn mẫu lớp 12: Phân tích bi kịch của Trương Ba trong tác phẩm Hồn trương ba, da hàng thịt
-
Văn mẫu lớp 12: Nghị luận về ý thức tôn trọng người khác (2 Dàn ý + 14 mẫu)
-
Văn mẫu lớp 9: Phân tích khổ cuối bài Sang thu của Hữu Thỉnh (Sơ đồ tư duy)
-
Văn mẫu lớp 9: Nghị luận ý nghĩa của sự lắng nghe
-
Văn mẫu lớp 12: Tổng hợp mở bài về tác phẩm Chiếc thuyền ngoài xa (71 mẫu)
-
Kể về một việc làm tốt của em (79 mẫu)
Xác thực tài khoản!
Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:
Số điện thoại chưa đúng định dạng!
Sắp xếp theo
