Đề thi thử THPT Quốc gia năm 2019 trường THPT Lê Hồng Phong, Thanh Hóa Đề thi minh họa THPT Quốc gia môn Toán
Bộ đề thi thử THPT Quốc gia năm 2019 trường THPT Lê Hồng Phong, Thanh Hóa được biên soạn nhằm giúp học sinh khối 12 củng cố lại các kiến thức lớp 10, lớp 11, đồng thời tiếp tục rèn luyện nâng cao kỹ năng giải Toán 12 để hướng đến kỳ thi THPT Quốc gia năm 2019.
Hy vọng đây là tài liệu bổ ích giúp các bạn học sinh lớp 12 rèn luyện kỹ năng làm bài và làm quen với cấu trúc đề thi môn Ngữ văn, Toán, Lịch sử, Hóa học, Vật lý. Chúc các bạn đạt được kết quả cao trong kỳ thi sắp tới.
Đề thi minh họa THPT Quốc gia môn Toán
SỞ GIÁO DỤC VÀ ĐÀO TẠO
THANH HÓA
TRƯỜNG THPT LÊ HỒNG PHONG
ĐỀ CHÍNH THỨC
(Đề thi có 6 trang)
ĐỀ THI THỬ THPT QUỐC GIA LẦN 4
KHỐI:12
NĂM HỌC 2018 -2019
Môn thi: TOÁN
Thời gian làm bài: 90 phút, không kể thời gian phát đề
Mã đề thi 001
Câu 1. Trong không gian với hệ toạ độ Oxyz, cho
−→
a = 2
−→
j −3
−→
k . Khi đó toạ độ của véc tơ
−→
a là
A. (2; 0; −3). B. (2; −3; 0). C. (0; 2; −3). D. (0; 2; 3).
Câu 2. Cho hàm số y = f (x) có bảng biến thiên như sau
x
y
0
y
−∞
−1
0
1
+∞
−
0
+
0
−
0
+
+∞+∞
−2−2
33
−2−2
+∞+∞
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
A. (1; +∞). B. (0; 1). C. (−1; 0). D. (−∞; 0).
Câu 3. Cho log
a
b = 2 và log
a
c = 3. Tính P = log
a
(b
2
c
3
).
A. P = 108. B. P = 30. C. P = 13. D. P = 31.
Câu 4. Trong không gian Oxyz, đường thẳng d :
x = 2 − t
y = 1 + 2t
z = 3 + t
có một véc-tơ chỉ phương là
A.
−→
u
2
= (2; 1; 1). B.
−→
u
3
= (2; 1; 3). C.
−→
u
4
= (−1; 2; 1). D.
−→
u
1
= (−1; 2; 3)..
Câu 5. Kí hiệu A
k
n
là số các chỉnh hợp chập k của n phần tử
(
1 ≤ k ≤ n
)
. Mệnh đề nào sau đây đúng ?
A. A
k
n
=
n!
(
n − k
)
!
. B. A
k
n
=
n!
(
n + k
)
!
. C. A
k
n
=
n!
k!
(
n − k
)
!
. D. A
k
n
=
n!
k!
(
n + k
)
!
.
Câu 6. Trong không gian Oxyz, mặt phẳng (P) : x + 2y + 3z − 5 = 0 có một véc-tơ pháp tuyến là
A.
−→
n
3
= (−1; 2; 3). B.
−→
n
1
= (3; 2; 1). C.
−→
n
4
= (1; 2; −3). D.
−→
n
2
= (1; 2; 3).
Câu 7.
Cho hàm số y = ax
3
+ bx
2
+ cx + d (a, b, c, d ∈ R) có đồ thị như hình vẽ bên. Số điểm
cực trị của hàm số đã cho là
A. 0. B. 2. C. 1. D. 3.
x
y
O
Câu 8. Số phức nào dưới đây là số thuần ảo ?
A. z = −2. B. z =
√
3 + i. C. z = 3i. D. z = −2 + 3i.
Câu 9. Thể tích V của hình lăng trụ có diện tích đáy S và chiều cao h được tính theo công thức nào sau
đây ?
A. V =
1
3
S.h. B. V =
1
2
S.h. C. V = S.h. D. V = 3S.h.
Câu 10. Tìm họ nguyên hàm F
x
của hàm số f
x
= 3 sin x +
2
x
.
A. F
x
= −3 cos x + 2 ln |x| + C. B. F
x
= 3 cos x + 2 ln |x| + C.
C. F
x
= 3 cos x − 2 ln |x| + C. D. F
x
= −3 cos x − 2 ln |x| + C.
Trang 1/6 Mã đề 001
Câu 11.
Đường cong trong hình vẽ bên là của hàm số nào dưới đây?
A. y = −x
4
+ 3x
2
− 1. B. y = −x
3
+ 3x
2
− 1.
C. y = x
4
− 3x
2
− 1. D. y = x
3
− 3x
2
− 1.
x
y
O
Câu 12. Cho
b
R
a
f (x) dx = −2 và
b
R
a
g(x) dx = 3. Tính I =
b
R
a
[2 f (x) − 3g(x)] dx.
A. I = −13. B. I = 13. C. I = −5. D. I = 5.
Câu 13. Cấp số cộng
(
u
n
)
có số hạng đầu u
1
= −5 và công sai d = 3. Tính u
15
.
A. u
15
= 47. B. u
15
= 57. C. u
15
= 27. D. u
15
= 37.
Câu 14. Diện tích mặt cầu bán kính R bằng
A. 4πR
2
. B. 2πR
2
. C. πR
2
. D.
4
3
πR
2
.
Câu 15. Tìm tập nghiệm S của phương trình log
2
x
2
− 4x + 3
= log
2
(
4x − 4
)
.
A. S =
{
1
}
. B. S =
{
7
}
. C. S =
{
1; 7
}
. D. S =
{
3; 7
}
.
Câu 16. Hàm số f (x ) có đạo hàm f
0
(x) = x
5
(2x + 2019)
4
(x −1). Số điểm cực trị của hàm số f (x) là
A. 2. B. 0. C. 1. D. 3.
Câu 17. Cho hình trụ có bán kính đáy 3 cm, đường cao 4 cm. Tính diện tích xung quanh của hình trụ.
A. 24π cm
2
. B. 36π cm
2
. C. 24 cm
2
. D. 36 cm
2
.
Câu 18. Trong không gian với hệ tọa độ Oxyz, tính khoảng cách từ điểm M(1; 2; −3) đến mặt phẳng
(P) : x + 2y − 2z − 2 = 0.
A. 1. B.
11
3
. C.
1
3
. D. 3.
Câu 19. Trong không gian Oxyz, viết phương trình mặt cầu tâm I
(
−2; 10; −4
)
và tiếp xúc với mặt phẳng
(
Oxz
)
.
A.
(
x + 2
)
2
+
(
y − 10
)
2
+
(
z + 4
)
2
= 100. B.
(
x + 2
)
2
+
(
y − 10
)
2
+
(
z + 4
)
2
= 10.
C.
(
x − 2
)
2
+
(
y + 10
)
2
+
(
z − 4
)
2
= 100. D.
(
x + 2
)
2
+
(
y − 10
)
2
+
(
z + 4
)
2
= 16.
Câu 20. Cho hàm số y = f (x) xác định, liên tục trên R và có bảng biến thiên như sau:
x
y
0
y
−∞
−2
0
+∞
+
0
−
0
+
−∞−∞
00
−4−4
+∞+∞
Tìm tập hợp tất cả các giá trị thực của tham số m sao cho phương trình f (x) = m − 1 có ba nghiệm thực
phân biệt.
A. (−4; 0). B. R. C. (−3; 1). D. [−3; 1].
Câu 21. Gọi S là diện tích hình phẳng giới hạn bởi các đường y = e
x
, y = 0, x = 0, x = 2. Mệnh đề nào
dưới đây đúng?
A. S = π
2
Z
0
e
2x
dx. B. S =
2
Z
0
e
2x
dx. C. S =
2
Z
0
e
x
dx. D. S = π
2
Z
0
e
x
dx.
Câu 22. Cho log
3
5 = a. Giá trị log
15
75 theo a là:
A.
1 + a
2 + a
. B.
1 − 2a
1 + a
. C.
1 + 2a
1 + a
. D.
1 − a
1 + a
.
Trang 2/6 Mã đề 001
Câu 23. Giá trị lớn nhất của hàm số y = x
4
− 4x
2
+ 9 trên đoạn [−2; 3] bằng
A. 201. B. 9. C. 2. D. 54.
Câu 24. Tập nghiệm của bất phương trình
√
2 + 1
x
2
+x
≥
√
2 − 1
2
là tập nào trong các tập sau?
A. (−∞; −2] ∪ [1, +∞). B. [−2; 1]. C. (−∞; −2) ∪ (1; +∞). D. R.
Câu 25.
Cho hàm số y = f (x) có bảng biến thiên
như hình dưới đây. Hỏi đồ thị của hàm số
đã cho có bao nhiêu tiệm cận?
A. 1. B. 3. C. 2. D. 4.
x
−∞
+∞
−2
0
y
0
+
−
y
+∞
1
−∞
0
Câu 26. Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A; AB = AC = a và có cạnh bên
S A vuông góc với đáy và S A = a
√
3. Tính thể tích của khối chóp.
A. V =
√
3a
3
6
. B. V = a
3
√
3. C. V =
√
3a
3
3
. D. V =
√
3a
3
2
.
Câu 27.
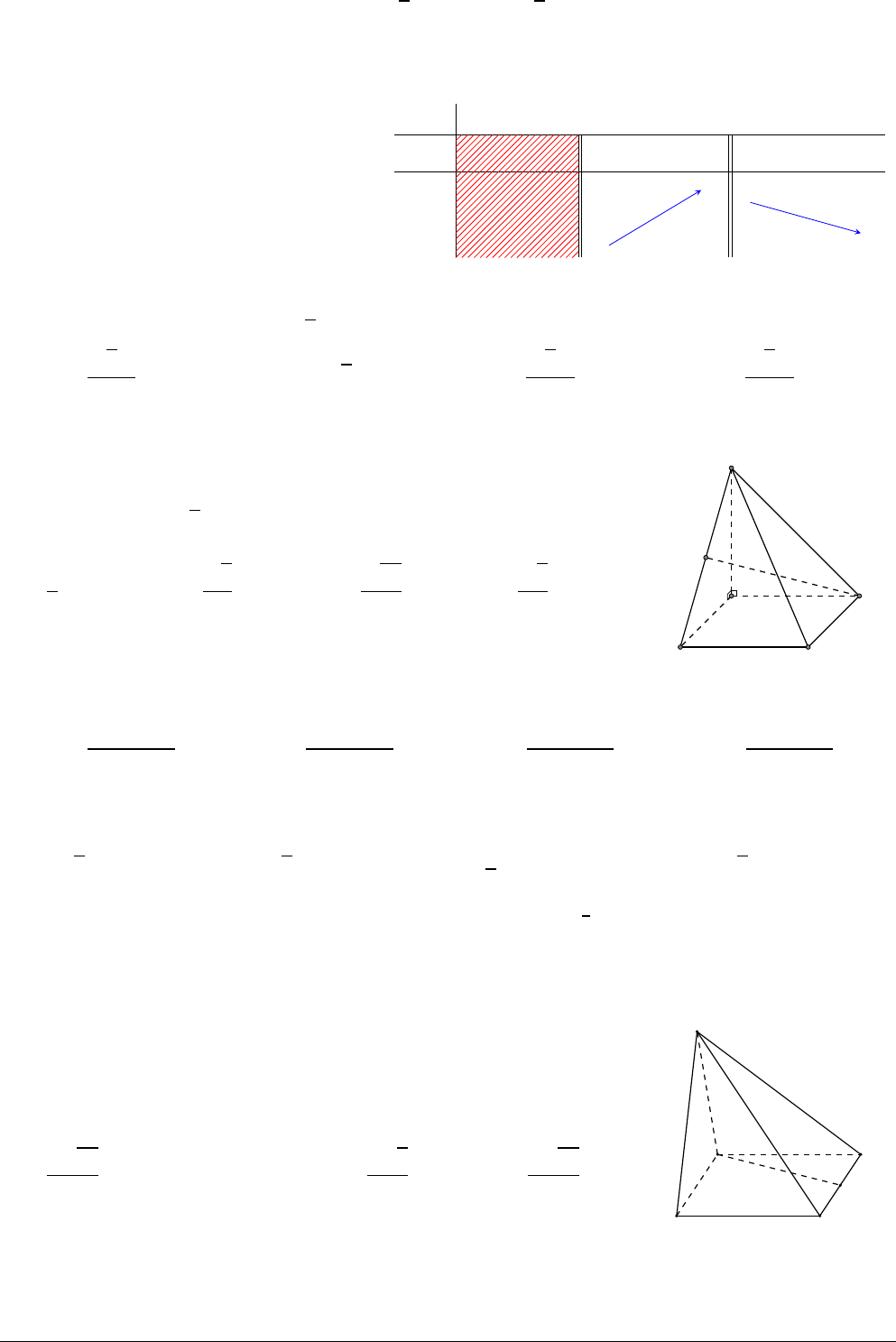
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a có S A ⊥
(ABCD) và S A = a
√
2. Gọi M là trung điểm S B (tham khảo hình vẽ bên).
Tính tan của góc giữa đường thẳng DM và (ABCD).
A.
2
5
. B.
√
5
5
. C.
√
10
5
. D.
√
2
5
.
A
B
M
C
D
S
Câu 28. Tìm đạo hàm của hàm số y = ln
x
2
+ x + 1
.
A. y
0
=
−
(
2x + 1
)
x
2
+ x + 1
. B. y
0
=
1
x
2
+ x + 1
. C. y
0
=
2x + 1
x
2
+ x + 1
. D. y
0
=
−1
x
2
+ x + 1
.
Câu 29. Gọi z
1
và z
2
là nghiệm phức của phương trình 4z
2
− 4z + 3 = 0 . Giá trị của biểu thức |z
2
1
| + |z
2
2
|
bằng:
A. 3
√
2. B.
√
3. C.
3
2
. D. 2
√
3.
Câu 30. Cho số phức z = a + bi (a, b ∈ R) thỏa mãn z
(
2i − 3
)
− 8i.z = −16 − 15i. Tính S = a + 3b.
A. S = 6. B. S = 5. C. S = 3. D. S = 4.
Câu 31.
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB = 2a, BC = a,
tam giác S AB là tam giác đều và nằm trong mặt phẳng vuông góc với đáy.
Gọi E là trung điểm của CD. Tính theo a khoảng cách giữa hai đường thẳng
BE và S C.
A.
a
√
30
10
. B. a. C.
a
√
3
2
. D.
a
√
15
5
.
B
A D
S
C
E
Câu 32. Một miếng tôn có dạng hình tròn bán kính 20 cm. Người ta cắt miếng tôn thành hai phần bằng
nhau và gò thành hai chiếc phễu.
Trang 3/6 Mã đề 001
Chia sẻ bởi: 
Trịnh Thị Thanh
Trịnh Thị Thanh Liên kết tải về
Link Download chính thức:
Đề thi thử THPT Quốc gia năm 2019 trường THPT Lê Hồng Phong, Thanh Hóa Download
Các phiên bản khác và liên quan:
Có thể bạn quan tâm
-
Văn mẫu lớp 9: Đóng vai ngư dân kể lại bài thơ Đoàn thuyền đánh cá
-
Bài thơ Lượm - Sáng tác năm 1949, Tố Hữu
-
Mẫu 09/ĐK: Đơn đăng ký biến động đất đai
-
Tranh tô màu Pikachu - Bộ tranh tô màu Pikachu đẹp
-
Giáo án Toán lớp 1 (Sách mới) - Giáo án Toán lớp 1 (trọn bộ 5 sách)
-
Tuyển tập đề thi học sinh giỏi môn Toán lớp 3
-
Thuyết minh về Thành Cổ Loa (2 Dàn ý + 5 mẫu)
-
Bộ tranh tô màu chủ đề gia đình cho bé
-
Văn mẫu lớp 10: Phân tích tác phẩm Hiền tài là nguyên khí của quốc gia (2 Dàn ý + 10 Mẫu)
-
Những vần thơ hay - Tuyển tập những bài thơ hay
Sắp xếp theo
