Bài toán cực trị hình học trong không gian Tài liệu ôn thi THPT Quốc gia môn Toán
Mời quý thầy cô giáo cùng các bạn học sinh lớp 12 cùng tham khảo tài liệu Bài toán cực trị hình học trong không gian được chúng tôi đăng tải ngay sau đây.
Bài toán cực trị hình học trong không gian trình bày phương pháp về các bài toán cực trị hình học trong không gian như: Tìm điểm, tìm độ dài để thể tích đa diện, độ dài đoạn thẳng đạt lớn nhất, nhỏ nhất, hướng dẫn phương pháp giải bài toán cực trị hình học không gian thông qua các ví dụ có lời giải chi tiết. Mời các bạn cùng tham khảo và tải tài liệu tại đây.
Bài toán cực trị hình học trong không gian
Sáng kiến kinh nghiệm năm học
Trường THPT Phù Cừ
Giáo viên; Quách Đăng Thăng - Tổ Toán - Tin 2
NỘI DUNG
I. CƠ SỞ LÝ THUYẾT
Muốn tìm giá trị lớn nhất hoặc giá trị nhỏ nhất của một đại lượng hình
học biến thiên f ta có thể sử dụng một trong các phương pháp sau:
1. Vận dụng các kết quả hình học cơ bản để so sánh trực tiếp f với một đại
lượng không đổi cho trước. Sau đây là một vài kết quả cơ bản:
a.
∀
A, B,C, AB + BC
≥
CA. Đẳng thức xảy ra khi và chỉ khi A, B, C thẳng
hàng theo thứ tự đó.
b. Nếu
ABC vuông tại A thì: AB < BC và AC < BC.
c. Trong một tam giác, đối diện với góc lớn hơn là cạnh lớn hơn và ngược lại.
d. Trong tất cả các đoạn thẳng vẽ từ một điểm M đến mặt phẳng
( )
α
(hoặc đường thẳng d) không chứa điểm M thì đoạn vuông góc là đoạn thẳng
ngắn nhất.
e. Đoạn thẳng vuông góc chung của hai đường thẳng chéo nhau là đoạn thẳng
ngắn nhất nối liền hai điểm lần lượt thuộc hai đường thẳng đó.
2. Nếu f được biểu thị thành một biểu thức của nhiều đại lượng biến thiên và
các đại lượng này lại được ràng buộc với nhau bởi một hệ thức liên hệ thì ta sử
dụng các bất đẳng thức đại số để tìm giá trị lớn nhất (giá trị nhỏ nhất) của f. Các
bất đẳng thức thường dùng là:
a. Bất đẳng thức Cô si:
∀
1 2
, ,
n
a a a
…
≥
0,
1 1
1 2
n
n
n
a a a
a a a
n
+ +
≥
…
…
Dấu đẳng thức xảy ra
⇔
1 1
n
a a a
= =
…
b. Bất đẳng thức Bu-nhi-a-côp-xki:
∀
1 2
, ,
n
a a a
…
,
1 2
, ,
n
x x x
…
,
2 2 2 2 2 2 2
1 1 2 2 1 1 2 2
( ) ( )( )( )
n n n n
a x a x a x a x a x a x
+ + ≤ + + +
…
Dấu bằng xảy ra khi
⇔
∃
k
∈
R,
1 1 2 2
, ,...,
n n
x ka x ka x ka
= = =
3. Nếu f được biểu thị bằng một hàm số của một biến số x thì ta sử dụng
phương pháp khảo sát hàm số để tìm giá trị lớn nhất (giá trị nhỏ nhất) của hàm
số đó trên miền xác định của nó, từ đó suy ra giá trị lớn nhất (giá trị nhỏ nhất)
của f.
4. Phương pháp tọa độ trong không gian
a. Trong không gian oxyz: Xét hệ toạ độ Đề các vuông góc giả sử A(x
1
,y
1
,z
1
),
B(x
2
,y
2
,z
2
) thì
1 2 2 1 2 1
( , , )
AB x x y y z z
= − − −
và
Sáng kiến kinh nghiệm năm học
Trường THPT Phù Cừ
Giáo viên; Quách Đăng Thăng - Tổ Toán - Tin 3
2 2 2
1 2 1 2 1 2
( ) ( ) ( )
AB x x y y z z= − + − + −
b. Cho 2 vectơ:
1 1 1
( , , )
u x y z
=
,
2 2 2
( , , )
v x y z
=
*
2 2 2
1 1 1
u x y z
= + +
;
2 2 2
2 2 2
v x y z
= + +
*
u v u v
+ ≤ +
(dấu “=” xảy ra khi và chỉ khi
,
u v
cùng chiều hoặc 1 trong 2
vectơ bằng
0
).
* Điều kiện để hai véc tơ
a
và
(
)
0
b b ≠
cùng phương là
t R
∃ ∈
để
a
=t
b
* Điều kiện để ba véc tơ
a
;
c
và
b
không đồng phẵng là
; . 0
a b c
≠
* Điều kiện để ba véc tơ
a
;
c
và
b
đồng phẵng là
; . 0
a b c
=
*
1 2 1 2 1 2
. 0 0
u v u v x x y y z z
⊥ ⇔ = ⇔ + + =
* Cho
ABC
Thì AB+BC
BC
≥
và
AB BC AC
− ≤
dấu đẳng thức sãy ra
khi ba điểm A;B;C thẳng hàng
II. MỘT SỐ BÀI TOÁN ĐIỂN HÌNH
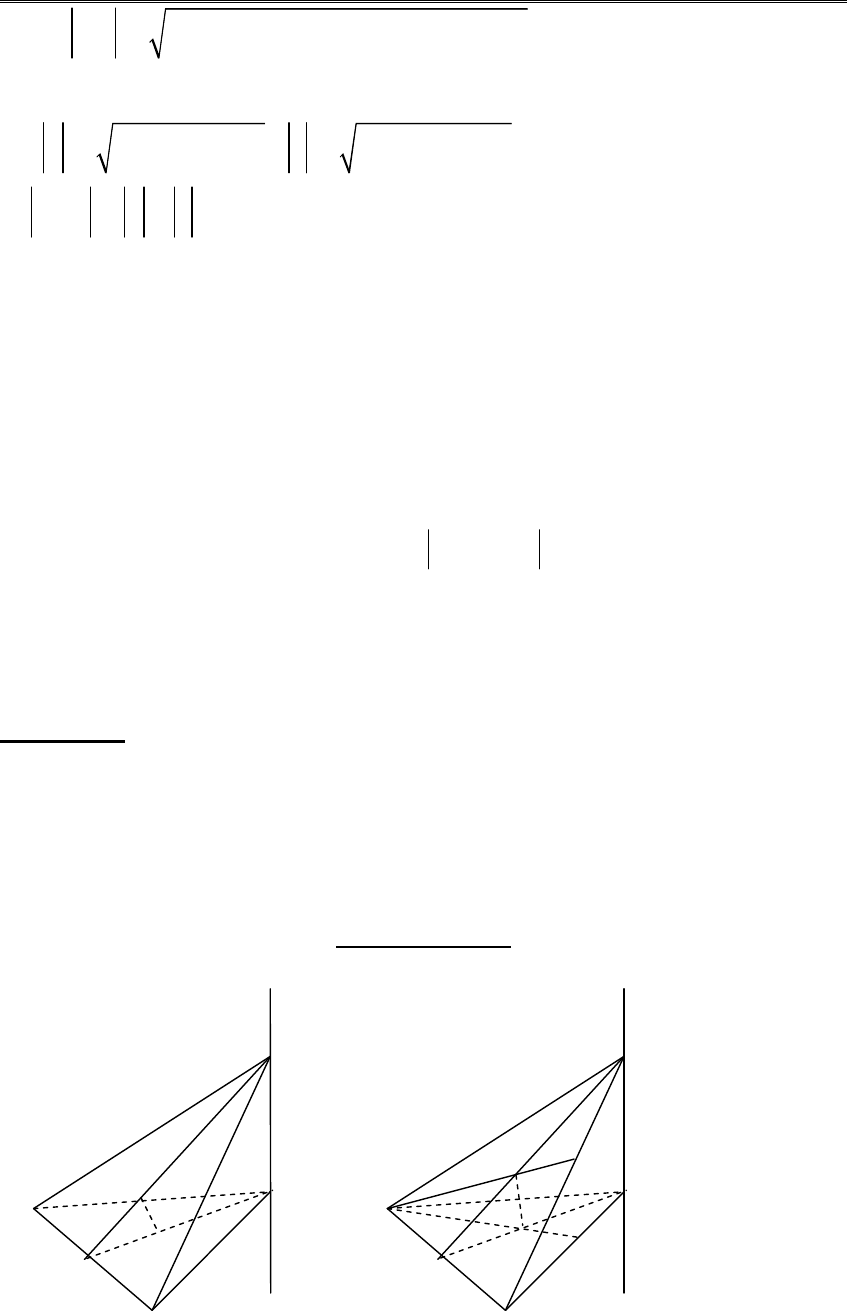
Bài toán 1: Cho tam giác cân ABC, AB=AC. Một điểm M thay đổi trên đường
thẳng vuông góc với mặt phẳng (ABC) tại A (M không trùng với điểm A)
a) Tìm quỹ tích trọng tâm G và trực tâm H của tam giác MBC
b) Gọi O là trực tâm của tam giác ABC, hãy xác định vị trí của M để thể tích tứ
diện OHBC đạt giá trị lớn nhất.
(Đại học Quốc gia Hà Nội - 1997)
Hướng dẫn giải
M
A
B
C
I
H
O
D
E
M
A
B
C
I
G
G’
Sáng kiến kinh nghiệm năm học
Trường THPT Phù Cừ
Giáo viên; Quách Đăng Thăng - Tổ Toán - Tin 4
a) Gọi I là trung điểm của BC, trọng tâm
∆
MBC là G, trọng tâm của ABC là
,
G
.
Trong
∆
MIA ta có :
,
1
3
IG IG
IM IA
= =
suy ra
,
GG
// MA
Do đó G nằm trên đường vuông góc với mặt phẳng (ABC) tại
,
G
, đó là đường
thẳng chứa
,
GG
.
Với MI và BD là đường cao với H là trực tâm
∆
ABC. Vì BE
⊥
CA và MA nên
BE
⊥
(MAC)
⇒
BE
⊥
MC (1)
BD là đường cao
MBC nên BD
⊥
MC (2)
Từ (1) và (2) suy ra MC
⊥
(BDE)
⇒
OH
⊥
MC (3)
Vì BC
⊥
MI và MA nên BC
⊥
(MAI)
⇒
BC
⊥
OH (4)
Từ (3) và (4) suy ra OH
⊥
(MBC)
⇒
HI
⊥
OH.
Vậy H nhìn đoạn cố định OI dưới một góc vuông
⇔
Quỹ tích H là đường tròn nằm trong mặt phẳng (MAI) có đường kính OI (trừ
hai điểm O và I)
b) Tứ diện OHBC có đáy OBC cố định nên thể tích lớn nhất khi H ở vị
trí “cao nhất” so với đáy OBC.
Xét
∆
OHI vuông khi góc
ABC
=
0
45
.
Hay
∆
OHI vuông cân
MAI
⇒
cân
⇒
AM =AI
Vậy khi AM =AI thì thể tích tứ diện OHBC lớn nhất.
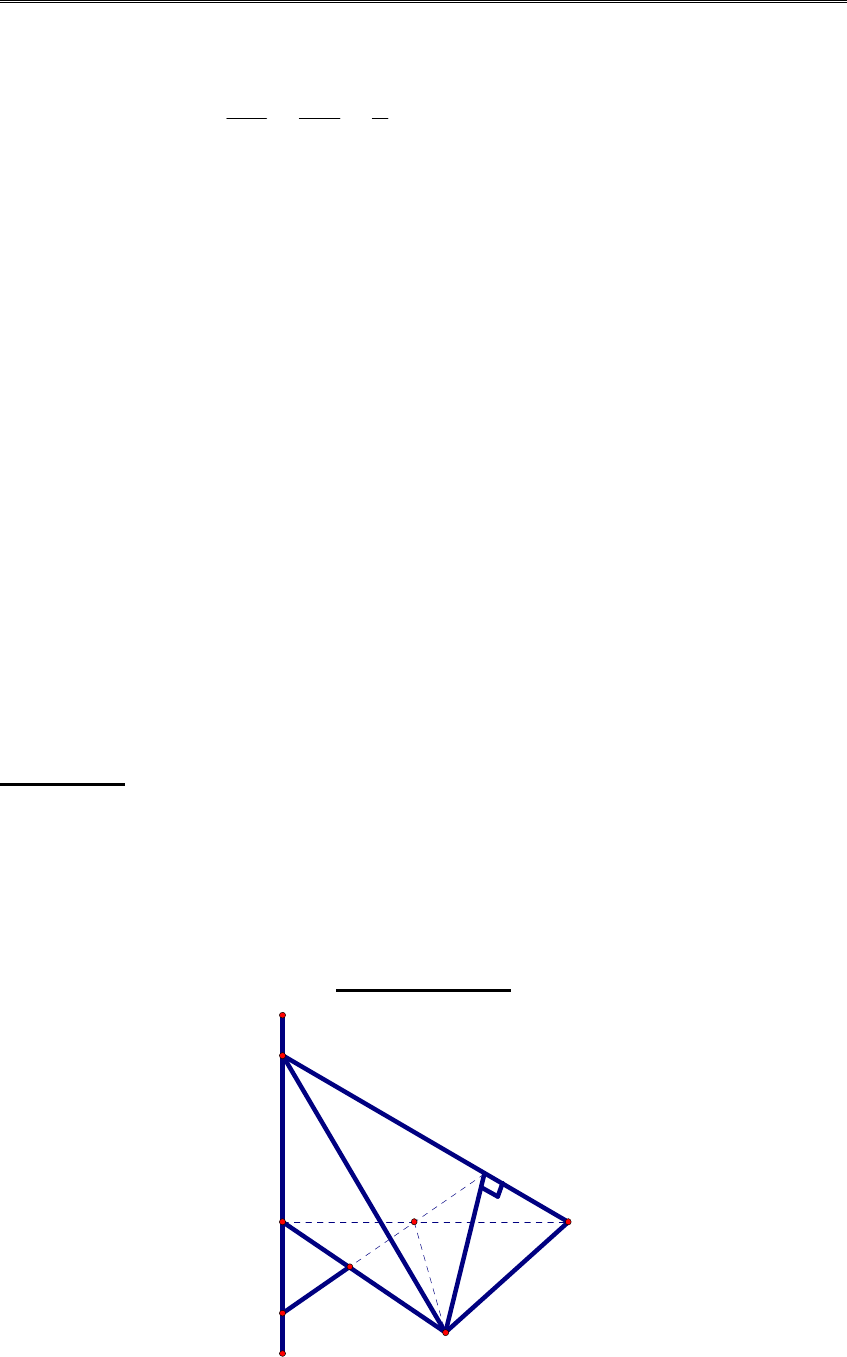
Bài toán 2: Cho tam giác đều OAB có cạnh bằng a > 0. Trên đường thẳng d đi
qua O và vuông góc với mp (OAB) lấy điểm M với OM = x. Gọi E, F lần lượt
là các hình chiếu vuông góc của A lên MB, OB. Trên đoạn thẳng EF cắt d tại N.
a)Chứng minh
AN BM
⊥
b)Xác định x để thể tích tứ diện ABMN là nhỏ nhất.
(Đại học Tổng hợp TP.HCM-1995)
Hướng dẫn giải
x
N
O
F
E
M
A
B
Chia sẻ bởi: 
Trịnh Thị Thanh
Trịnh Thị Thanh Liên kết tải về
Link Download chính thức:
Bài toán cực trị hình học trong không gian Download
Có thể bạn quan tâm
-
Mẫu 09/ĐK: Đơn đăng ký biến động đất đai
-
Tranh tô màu Pikachu - Bộ tranh tô màu Pikachu đẹp
-
Giáo án Toán lớp 1 (Sách mới) - Giáo án Toán lớp 1 (trọn bộ 5 sách)
-
Tuyển tập đề thi học sinh giỏi môn Toán lớp 3
-
Thuyết minh về Thành Cổ Loa (2 Dàn ý + 5 mẫu)
-
Bộ tranh tô màu chủ đề gia đình cho bé
-
Văn mẫu lớp 10: Phân tích tác phẩm Hiền tài là nguyên khí của quốc gia (2 Dàn ý + 10 Mẫu)
-
Những vần thơ hay - Tuyển tập những bài thơ hay
-
Văn mẫu lớp 9: Nghị luận về hiện tượng học tủ, học vẹt
-
File luyện viết chữ in hoa - Mẫu chữ hoa cho học sinh Tiểu học
Sắp xếp theo
