Ôn thi Đại học môn Toán - Chuyên đề: Lượng giác Đề thi Toán lượng giác
ÔN THI ĐẠI HỌC MÔN TOÁN CHUYÊN ĐỀ: LƯỢNG GIÁC
VẤN ĐỀ 1: PHƯƠNG TRÌNH LƯỢNG GIÁC
A. PHƯƠNG PHÁP GIẢI
I. Phương trình lượng giác cơ bản
* cosx = cosα ↔ x = ± α + k2π
* 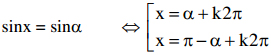
* tanx = tanα ↔ x = α + kπ
* cotx = cotα ↔ x = α + kπ
Với k thuộc Z
II. Phương trình bậc hai đối với một hàm số lượng giác
* asin2x + bsinx + c = 0. Đặt t = sinx, |t| ≤ 1
* acos2x + bcosx + c = 0. Đặt t = cosx, |t| ≤ 1
* atan2x + btanx + c = 0. Đặt t = tanx
* acot2x + bcotx + c = 0. Đặt t = cotx
III. Phương trình bậc nhất đối với sinx, cosx
asinx + bcosx = c (*)
Điều kiện có nghiệm: a2 + b2 ≥ c2
Cách 1:
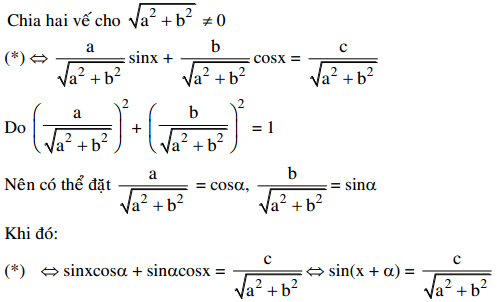
Cách 2:
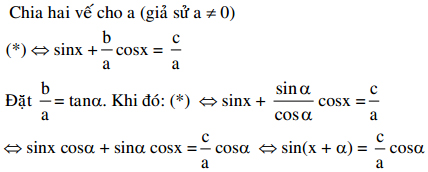
Cách 3:
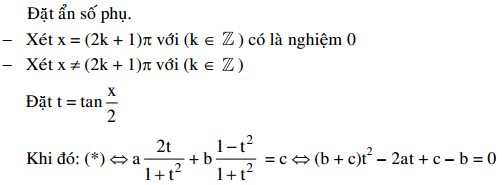
IV. Phương trình đối xứng: a(sinx + cosx) + bsinxcosx + c = 0
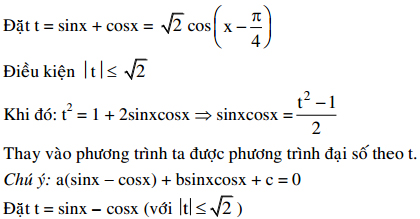
V. Phương trình đẳng cấp bậc 2 đối với sinx, cosx
asin2x + bsinxcosx + ccos2x = 0
- Xét cosx = 0 ↔ x = π/2 + kπ (k thuộc Z) có là nghiệm không?
- Xét cosx # 0. Chia 2 vế cho cos2x ta thu được phương trình bậc 2 theo tanx.
Chú ý: Nếu là phương trình đẳng cấp bậc k đối với sinx, cosx thì ta xét cosx = 0 và xét cosx # 0 chia 2 vế của phương trình cho coskx và ta thu được một phương trình bậc k theo tanx
B. ĐỀ THI
Bài 1: Đại học khối A năm 2011
Giải phương trình:c![]()
Giải:
Điều kiện: sinx # 0. Khi đó:
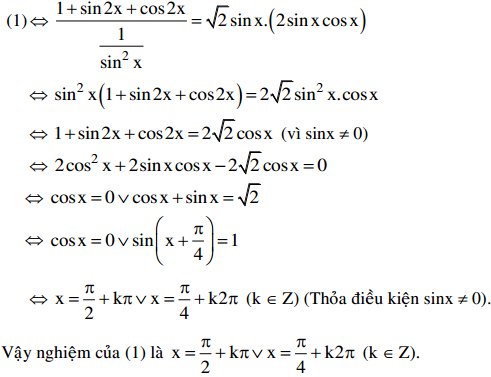
Bài 2: Đại học khối B năm 2011
Giải phương trình: sin2x.cosx + sinx.cosx = cos2x + sinx + cosx
Giải:
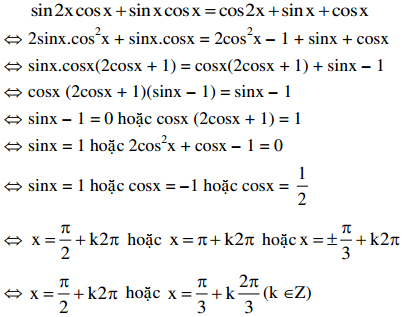
Bài 3: Đại học khối D năm 2011
Giải phương trình: 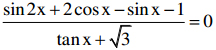

Download tài liệu để xem chi tiết.
Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:












 Lớp 2
Lớp 2
 Lớp 4
Lớp 4
 Lớp 5
Lớp 5
 Thi vào 6
Thi vào 6
 Lớp 6
Lớp 6
 Lớp 7
Lớp 7
 Lớp 9
Lớp 9









