Đề thi Olympic Toán sinh viên năm 2014 Toán - Đại số và Giải tích
HỘI TOÁN HỌC VIỆT NAM |
ĐỀ THI OLYMPIC TOÁN SINH VIÊN NĂM 2014Môn thi: Giải tích |
Câu 1.
Cho dãy số (un) thỏa mãn u1 = 1 và ![]() ; trong đó a ≥ 0. Tìm a sao cho (un) hội tụ và tìm giới hạn đó.
; trong đó a ≥ 0. Tìm a sao cho (un) hội tụ và tìm giới hạn đó.
Câu 2.
Cho hai hàm f(x) và g(x) xác định trên R và thỏa mãn điều kiện (f(x) − f(y))(g(x) − g(y)) = 0 với mọi x; y ∈ R.
Chứng minh ít nhất một trong hai hàm f hoặc g là hàm hằng.
Câu 3.
1) Cho hàm số f đơn điệu trên [0;∞) và 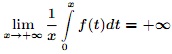
Chứng minh rằng: ![]()
2) Kết luận trên còn đúng không khi f là hàm liên tục trên [0;∞) nhưng không đơn điệu trên khoảng đó? Tại sao?
Câu 4.
Tìm tất cả các hàm số f(x) xác định, liên tục trên đoạn [0; 1], khả vi trong khoảng (0; 1) và thỏa mãn điều kiện:
![]()
Câu 5.
Cho dãy số (xn) được xác định bởi ![]()
Tìm ![]() với điều kiện x0 ≥ 4; x1 ≥ 4.
với điều kiện x0 ≥ 4; x1 ≥ 4.
Câu 6. Thí sinh chọn một trong hai câu:
6a. Cho (an) là dãy số xác định bởi
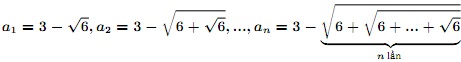
Hãy chứng minh rằng chuỗi số hội tụ.
6b. Cho f là hàm số liên tục trên [0;+∞). Giả sử rằng
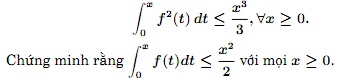
Download tài liệu để xem chi tiết.
Chọn file cần tải:
Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:












 Lớp 2
Lớp 2
 Lớp 4
Lớp 4
 Lớp 5
Lớp 5
 Thi vào 6
Thi vào 6
 Lớp 6
Lớp 6
 Lớp 7
Lớp 7
 Lớp 9
Lớp 9